

Other symbols. Loading [MathJax]/jax/element/mml/optable/MathOperators.js Produced by Charles Wells Revised 2015-12-24 Introduction to this website website TOC website indexblog head of Symbolic Language chapter Contents Introduction This list includes only the major meanings of the most common symbols, according to my judgment.The list of mathematical symbols in Wikipedia includes many other symbols but does not include all, or even most of, the meanings of the symbols.Like many other parts of abstractmath.org, in depth lexicographical research is needed (anyone have ten million dollars?)

See Remarks about usage. Accented characters Mathematicians frequently use an accent to create a new variable from an old one. The most commonly used accents over the letter are arrow, bar, check, dot, hat and tilde. prime and star may be used after the letter as a superscript. slash may be used across a relational symbol. All of the accents except arrow and slash (as far as I know) have more than one meaning. Arrow Bar. Isomorphism theorem - Wikipedia. Proof verification - Let $G$ be a group and $H$ a normal subgroup of $G$. Prove: $x^2 \in H$ for every $x \in G$ iff every element of $G/H$ is its own inverse. Discrete Mathematics Quick Guide. Continuous Mathematics is based upon continuous number line or the real numbers.

It is characterized by the fact that between any two numbers, there are almost always an infinite set of numbers. For example, a function in continuous mathematics can be plotted in a smooth curve without breaks. Discrete Mathematics, on the other hand, involves distinct values; i.e. between any two points, there are a countable number of points. Prove phi(f):F(R)->R given by phi(f)=f(0) is a homomorphism? Abstract algebra - Prove the following is a homomorphism and describe its kernel.
Abstract Algebra Cheat Sheet. Definition:Group Homomorphism - ProofWiki. Surjective function - Wikipedia. A surjective function from domainX to codomainY. The function is surjective because every point in the codomain is the value of f(x) for at least one point x in the domain. Any function induces a surjection by restricting its codomain to its range. Every surjective function has a right inverse, and every function with a right inverse is necessarily a surjection.
The composite of surjective functions is always surjective. Any function can be decomposed into a surjection and an injection. Definition[edit] Abstract algebra - Let $H$ have order $m$ and $K$ have order $n$, where $m$ and $n$ are relatively prime. Then $H \cap K=\{e\}$ Abstract algebra - Determine all subgroups of $\mathbb{R}^*$ (nonzero reals under multiplication) of index $2$.
Describe the coset of the Subgroup. #1.) Z of R. AND #2.) the subgroup H={(x,y):x=y} of RxR.? Abstract algebra - Find the Cosets of Subgroup $\langle 3 \rangle $ of $\mathbb{Z}$ Abstract algebra - Describe the cosets of the subgroup $\langle 3\rangle$ of $\mathbb{Z}$ Abstract algebra - List Elements of Left/Right Cosets of $H$ for: $G=\mathbb{Z}_{15}, H=\langle 5 \rangle. Abstract algebra - Let a~b iff there is an $x \in G$ such that $a=xbx^{-1}$ Some other set notation We will use the notation to mean that e is an element of A. We will use the notation to mean that e is not an element of A. - ppt download. Set Notation Union Subset Intersection Null or Empty Set Element Not an Element Not a Subset. - ppt download. Abstract Algebra/Sets. Elementary number theory - In $\mathbb{Z}$, let m~n iff m-n is a multiple of 10. Physics Forums - The Fusion of Science and Community. Prove that the following is an equivalence relation on the indicated set.
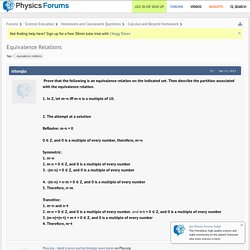
Then describe the partition associated with the equivalence relation. 1. If GxH is a cyclic group, then prove that G and H are cyclic? Let G and H be groups with a E G and b E H. Prove that if (a,b) is a generator of G x H then a is a generator of G and b is a generator of H? Abstract algebra - If $G = \langle a\rangle$ and $b$ $\in$ $G$, the order of $b$ is a factor of the order of $a$ Abstract algebra - Elementary Properties of cyclic groups. Physics Forums - The Fusion of Science and Community. 1.
The problem statement, all variables and given/known data As the title suggests - this is very simple, I only want to check. Elements which correspond under an isomorphism. View topic - Elements whch correspond under an isomorphism. Exercise of Algebra. Ask Dr. Math. D. D1.

If ap = e where p is a prime number , then a has order p. ( a e.) Proof. Any element and its inverse have the same order. - My Math Forum. If a,b,c are elements in group G. Prove, if ord(a)=n , then a^(n-r)=(a^r)^-1? View topic - Elements whch correspond under an isomorphism. DgrayMan wrote: i wish i was a math genius like you guys, but im not. i struggle with the obvious.
It's kind of like being asked a question such as "how old you are? " in a foreign language. AATA Front Matter. Is a group uniquely determined by the sets {ab,ba} for each pair of elements a and b? Help with Permutations? PermutationsAsTrees. Peter Luschny, 2010-07-20 Contents * 1 Permutation Trees o 1.1 Definitions o 1.2 Example classifications * 2 Permutation trees with power 4 * 3 Counting permutation trees o 3.1 A008292 Permutation trees of power n and width k. o 3.2 A179454 Permutation trees of power n and height k. o 3.3 A179455 Permutation trees of power n and height does not exceed k. o 3.4 A179456 Permutation trees of power n and height at least k. o 3.5 A179457 Permutation trees of power n and width does not exceed k. * 4 The correspondence: Permutation <-> Tree o 4.1 Given a permutation, how to construct the associated rooted tree?

O 4.2 Given a rooted tree, how to construct the associated permutation? * 5 Flattening the tree: the caterpillar notation. * 6 Summary: Three classifications of permutation trees. * 7 The permutation trees with power 5 Definitions A permutation tree is a labeled rooted tree that has vertex set {0,1,2,.. Example classifications A008292, Permutation trees of power n and width k. Links. List of mathematical symbols by subject - Wikipedia.
GroupTheory. Note: You are looking at a static copy of the former PineWiki site, used for class notes by James Aspnes from 2003 to 2012.

Many mathematical formulas are broken, and there are likely to be other bugs as well. These will most likely not be fixed. You may be able to find more up-to-date versions of some of these notes at A group is an algebra (see AlgebraicStructures) with an associative binary operation (usually written as either multiplication or addition), a constant identity element e such that ex = xe = x for all x, and an inverse operation x -> x-1 such that xx-1 = x-1x = e for all x.
If it is also the case that xy=yx for all x and y, the group is abelian. Permutations - Prove that if the identity is written as the product of $r$ transpositions, then $r$ is an even number. Group theory - Prove this is a subgroup: Subset of $S(A)$ consisting of all the permutations $f(a) = a$ Properties of permutation of a set. Chapter 14: Mathematical Foundations - SWEBOK. Introduction Software professionals live with programs.
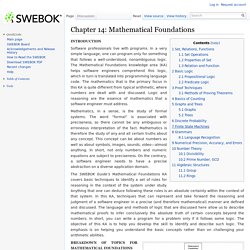
In a very simple language, one can program only for something that follows a well-understood, nonambiguous logic. The Mathematical Foundations knowledge area (KA) helps software engineers comprehend this logic, which in turn is translated into programming language code. The mathematics that is the primary focus in this KA is quite different from typical arithmetic, where numbers are dealt with and discussed. Logic and reasoning are the essence of mathematics that a software engineer must address. Mathematics, in a sense, is the study of formal systems. The SWEBOK Guide’s Mathematical Foundations KA covers basic techniques to identify a set of rules for reasoning in the context of the system under study. Figure 14.1: Breakdown of Topics for the Mathematical Foundations KA.
Subgroup - Wikipedia. Set symbols of set theory (Ø,U,{},∈,...) Physics Forums - The Fusion of Science and Community. 1.
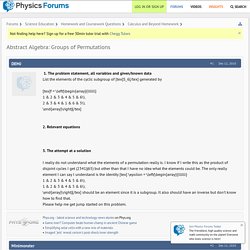
The problem statement, all variables and given/known data List the elements of the cyclic subgroup of [tex]S_6[/tex] generated by [tex]f = \left(\begin{array}{llllll} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 4 & 1 & 6 & 5\\ \end{array}\right)[/tex]2. Relevant equations3. The attempt at a solution I really do not understand what the elements of a permutation really is. I know if I write this as the product of disjoint cycles I get (2341)(65) but other than that I have no idea what the elements could be.
The only really element I can say I understand is the identity [tex] \epsilon = \left(\begin{array}{llllll} 1 & 2 & 3 & 4 & 5 & 6\\ 1 & 2 & 3 & 4 & 5 & 6\\ \end{array}\right)[/tex] should be an element since it is a subgroup. Abstract algebra - List the elements of the cyclic subgroup of $S_6$ Write Out The Operation Table For The Group S4/V. Working with Permutations in Wolfram. Permutations are among the most basic elements of discrete mathematics. They are used to represent discrete groups of transformations, and in particular play a key role in group theory, the mathematical study of symmetry. Permutations and groups are important in many aspects of life. We all live on a giant sphere (the Earth) whose rotations are described by the group SO(3) (the special orthogonal group in 3 dimensions).
On the micro-scale, the Hungarian-American physicist Eugene Wigner (November 17, 1902–January 1, 1995), who received a share of the Nobel Prize in Physics in 1963, discovered the “electron permutation group”, one of many applications of permutation groups to quantum mechanics. Permutations deserve a full treatment in Wolfram|Alpha. Let’s first define permutations, then discuss how to work with them in Wolfram|Alpha. We call this two-line notation. Alpha Examples: Permutations. Symmetric group:S5 - Groupprops.
Introduction to Groups and Permutation Groups. Permutation (1 2 3) Is 71864 An Even Number? - Math Question [SOLVED] View topic - Functions on Arbitrary Sets and Groups. Find A Bijective Function F From The Set Z Of The. Real analysis - Determine whether the following function is (a) injective and (b) surjective. Injective, Surjective and Bijective. "Injective, Surjective and Bijective" tells us about how a function behaves. A function is a way of matching the members of a set "A" to a set "B": A General Function points from each member of "A" to a member of "B". A function never has one "A" pointing to more than one "B", so one-to-many is not OK in a function (so something like "f(x) = 7 or 9" is not allowed) But more than one "A" can point to the same "B" (many-to-one is OK) Injective means that every member of "A" has its own unique matching member in "B".
Khanacademy. Group (mathematics) - Wikipedia. TriangleGroup. Undefined The Symmetry Group of the Triangle There are six motions that can bring an equilateral triangle back into its original position. They are Do nothing Rotate 120 degrees counterclockwise Rotate 240 degrees counterclockwise Flip about the symmetry axis through the upper vertex Flip about the symmetry axis through the lower left-hand vertex Flip about the symmetry axis through the lower right-hand vertex There are other motions but they are "equivalent" to those listed above. For example rotating the triangle 360 degrees is "equivalent" to doing nothing since the basic orientation of the triangle is unchanged.
We've labelled the vertices A, B and C and have shown the 6 symmetry motions below: The equilateral triangle before a movement and after any movement that doesn't change anything (like rotating it 360 degrees). Abstract algebra - If $ab=ba$, Prove $a^2$ commutes with $b^2$ Subgroups of functions and of abelian groups. Excercises. - xkcd. You haven't finished this part yet (one small step to go). Abstract algeebra: problems on generator of groups? 1) i claim <6,9> = <3> = <9> = {0,3,6,9} Abstract algebra - Determine whether or not H is a subgroup of G. If ab=ba, then (ab)^n =(a^n)(b^n) for every positive integer n. prove by induction.? Direct product of Groups - xkcd. So for this part: List the elements of Z2xZ3, and write its operation table.
Abstract algebra - Prove that every group of order $4$ is abelian. Explain Why Every Row Of A Group Table Must Contai... Abstract algebra - Fill in a group table. Group Theory for puzzles. Lemma 6.5: Let n=|G| and let ki be the order of the poles in the i-th orbit of the G-action on the set of poles. From Wolfram MathWorld. In celestial mechanics, the fixed path a planet traces as it moves around the sun is called an orbit. Project Crazy Project. Solutions to exercises from Abstract Algebra by Dummit & Foote. (Not all links are active.) Solutions. Abstract Algebra Solutions. A Concrete Approach to Abstract Algebra: From the Integers to the ... - Jeffrey Bergen - Google Books. Group (mathematics)
This article is about basic notions of groups in mathematics. For a more advanced treatment, see Group theory. Groups share a fundamental kinship with the notion of symmetry. For example, a symmetry group encodes symmetry features of a geometrical object: the group consists of the set of transformations that leave the object unchanged and the operation of combining two such transformations by performing one after the other. Lie groups are the symmetry groups used in the Standard Model of particle physics; Point groups are used to help understand symmetry phenomena in molecular chemistry; and Poincaré groups can express the physical symmetry underlying special relativity. Proofs and Such: R X R is a field. Consider R X R with the usual coordinatewise addition and a new multiplication given by. Why is (a,b) * (c,d) = (ac-bd, ad+bc)?
I assume that you are referring to multiplication on ℂ, the system of complex numbers. The rule for multiplication of complex numbers is motivated by this: Number Systems with Different Kinds of Numbers. ABSTRACT ALGEBRA: A Study Guide for Beginners. John A. Beachy. ABSTRACT ALGEBRA: OnLine Study Guide, Table of Contents. These online notes are for students who are working through our textbook Abstract Algebra. The notes are focused on solved problems, which are numbered consecutively, beginning with the exercises in the text.
Our intention is to help students learn how to do proofs as well as computations. There are also some "lab" questions on groups, based on a Java applet Groups15 written by John Wavrik of UCSD. ABSTRACT ALGEBRA ON LINE. ABSTRACT ALGEBRA: OnLine Study Guide, Section 3.1. Abstract Algebra Cheat Sheet.