

Lien roues carrées et arche en chaînette. CHAÎNETTECatenary or funicular curve, Kettenlinie La chaînette est la forme prise par un fil pesant flexible infiniment mince homogène inextensible suspendu entre deux points, placé dans un champ de pesanteur uniforme ; Galilée pensait que c'était un arc de parabole, mais Leibniz, Jean Bernoulli, et Huygens ont montré en 1691, indépendamment, qu'il n'en était rien.
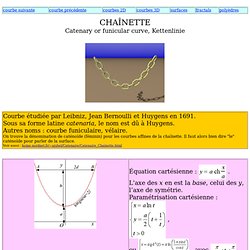
Apprenons à différencier les chaînettes des paraboles : Voir la courbe du pont suspendu, ainsi que la chaînette élastique, qui joignent la parabole à la chaînette.Comme pour le fil suspendu, une voûte formée de pierres jointives tenant par leur propre poids prend aussi une forme de chaînette, renversée (propriété dite de la voûte de Poinsot - démonstration Brocard part. comp. p 189) : Par contre, les arches des ponts ont, elles, un profil parabolique (pont suspendu à l'envers...) Le viaduc de Garabit a une arche parabolique (et non circulaire comme le disent les cartes postales) Sont-ce des chaînettes ? Les roues carrées. Chaînettes aériennes. Pour trouver son équation, on écrit l'équilibre d'un morceau de chaînette de longueur l entre le point le plus bas (O) et un point quelconque (M).
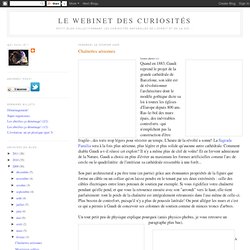
La tension en ces points vaut respectivement T(O) et T(M) et le poids de cette longueur de chaînette vaut P(l), vertical et proportionnel à la longueur l (en gras ce sont des vecteurs):T(O)+T(M)+P(l)=0. P est vertical et T(O) est horizontal, et T(M) est tangent à la courbe en M (c'est une tension qui s'exerce dans l'alignement de la chaînette).
Bref, la forme est peut-être naturelle, mais l'équation n'est pas ultra simple: c'est une courbe transcendante, impossible à tracer à la règle et au compas (à moins qu'El_Jj ne nous trouve une méthode révolutionnaire avec des pliages?) Et encore, là nous n'avons vu que la courbe en deux dimensions: dans la vraie vie on doit fabriquer des voûtes en trois dimensions! Pour la tracer précisément sur un plan, bon courage. Fonction hyperbolique. Un article de Wikipédia, l'encyclopédie libre.
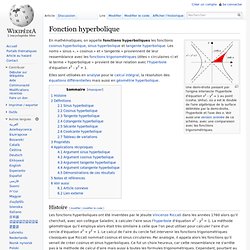
Une demi-droite passant par l'origine intersecte l'hyperbole d'équation x2 – y2 = 1 au point (cosha, sinha), où a est le double de l'aire algébrique de la surface délimitée par la demi-droite, l'hyperbole et l'axe des x. Voir aussi une version animée de ce schéma, avec une comparaison avec les fonctions trigonométriques.
Histoire[modifier | modifier le code] Définitions[modifier | modifier le code] Les fonctions hyperboliques sont analogues aux fonctions trigonométriques ou fonctions circulaires. Sinus hyperbolique Cosinus hyperbolique Tangente hyperbolique Sinus hyperbolique[modifier | modifier le code] Définie comme étant la partie impaire de la fonction exponentielle, c’est-à-dire par : sinh — ou sh — est une bijection de classe C∞ de ℝ dans ℝ strictement croissante, et impaire. Cosinus hyperbolique[modifier | modifier le code]