

Latency Tricks. By: Clark Gaebel [web] [keybase] [email] Special thanks to reviewers: Ben Foppa [keybase], Norm Tasfi [web] [twitter] The Setup¶ Servers take time to respond to messages.

Lyra. Flexible Business Intelligence. Neural networks and deep learning. One of the most striking facts about neural networks is that they can compute any function at all.
That is, suppose someone hands you some complicated, wiggly function, f(x): No matter what the function, there is guaranteed to be a neural network so that for every possible input, x, the value f(x) (or some close approximation) is output from the network, e.g. An Interactive Introduction to Graphics Programming. This is a proposal and proof-of-concept for an interactive book about programming the graphics processor.

Modern computers come with two separate processors, two “brains”: The traditional CPU, the Central Processing Unit The newer GPU, the Graphics Processing Unit Almost all books and courses about programming only teach you how to program the CPU. GPU programming is esoteric. Learning resources are targeted at experienced programmers who need to use the GPU for applications like high-performance video games and scientific simulations.
Yet there is a unique joy to programming the graphics processor. This book is intended to bring the wonder and joy of graphics processor programming to a wider audience. An Interactive Book This book will be interactive. The text will be extensively illustrated with manipulable diagrams and live code examples. The Thermodynamic Ice Bag. Dear Readers, We’ve reached chapter 3 of the serial on the film cooling system of the TM65LE, and here we’ll take a closer look at the contents of the thermodynamic ice packet.

Specifically, the options a rocket engine designer can chose from when it’s realized that the heat flux is far from optimal. In classic rocket engines, such as TM65LE, for a given fuel type there’s basically four methods for controlling the heat flux in an engine with a long burn time; radiation, ablative cooling, regenerative cooling, and film cooling.
Probabilistic Models of Cognition. IDE. IDE. Aurora (StrangeLoop 2013 demo) Visually stunning math concepts which are easy to explain. Models help you understand why you disagree. Models help you understand why you disagree In a blog post yesterday, I advocated very strongly that rather than simply bloviating about political (and other) topics, we should instead build mathematical models to clearly express our thinking.
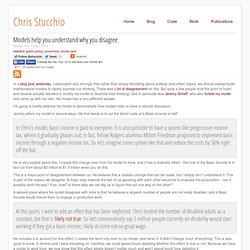
There was a lot of disagreement on this. But quite a few people took the point to heart, and several actually decided to modify my model to illustrate their thinking. One in particular was Jeremy Scheff, who who forked my model and came up with his own. His model has a very different answer. I’m going to briefly address his model to demonstrate how models help us have a rational discussion. Jeremy alters my model in several ways. In Chris’s model, basic income is paid to everyone. Developer API. Reinventing Explanation.
The Babylonian Map of the World is one of the world's oldest extant maps, dating to 600 BCE.

It's a crude map, difficult to read at a glance, but fortunately an accompanying cuneiform text describes the features on the map, including Babylon, seven other cities, a canal, and a mountain: Modern maps are, of course, far better than this early map. They improve on it by taking advantage of the many map-making techniques developed since 600 BCE, such as: surveying to get proportions correct; projections to correct for the curvature of the Earth; methods to depict topographic features; and so on. Storytelling with Data. Feb. 28, 2013 This is a condensed version of my opening keynote at the Tapestry Conference, which was held yesterday in Nashville’s beautiful Union Station Hotel.
I’m writing this from memory so at best it will only be an approximation of what I said. Thanks to all the organizers and attendees for a great event. Scrubbing Calculator. Bret Victor / May 31, 2011 This page presents an idea for exploring practical algebraic problems without using symbolic variables. I call this tool a "scrubbing calculator", because you solve problems by interactively scrubbing over numbers until you're happy with the results. Nbviewer.ipython.org/url/norvig.com/ipython/Economics. Now let's describe the code to run the simulation and summarize/plot the results.
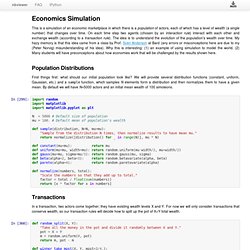
The function simulate does the work; it runs the interaction function to find two actors, then calls the transaction function to figure out how to split their wealth, and repeats this T times. The only other thing it does is record results. Data Structure Visualization. Calca - The Text Editor that Loves Math. Andart: Torus–Earth. Torus–Earth One question at Io9 that came up when they published my Double Earth analysis was "What about a toroidal Earth?
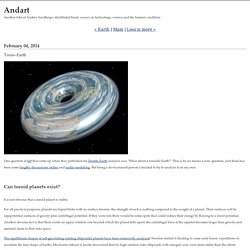
" Starship Radiators. Looking at the Daedalus starship, it might appear at first glance that the ship has no radiators.
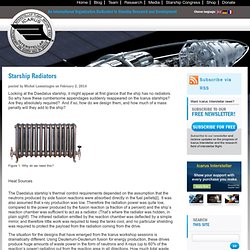
So why have these cumbersome appendages suddenly reappeared on the Icarus starships? Are they absolutely required? And if so, how do we design them, and how much of a mass penalty will they add to the ship?