

Fast Fourier transform — FFT — Librow — Software development. Article 10 Category.
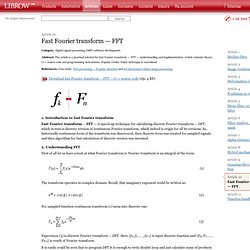
Digital signal processing (DSP) software development. Abstract. Discrete Fourier transform. Relationship between the (continuous) Fourier transform and the discrete Fourier transform.
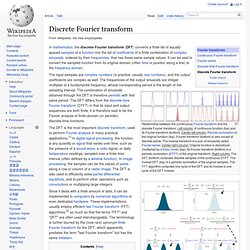
Left column: A continuous function (top) and its Fourier transform (bottom). Center-left column:Periodic summation of the original function (top). Fourier transform (bottom) is zero except at discrete points. Discrete Fourier Transform Tutorial. FFTW Home Page. The DFT “à Pied”: Mastering The Fourier Transform in One Day : The DSP Dimension.