

Un tour de magie mathématique… Ce que je vais vous apprendre dans cet article va changer votre vie.
Vous allez passer de simple inconnu banal à star mondiale de la magie. Vous allez faire passer David Copperfield pour un amateur. Aller, trêve de publicité mensongère et d’accroche gratuitement racoleuse, je vais vous présenter un petit tour de magie mathématique bien sympathique. La seule chose dont vous aurez besoin, ce sont les 10 cartes suivantes (que j’ai confectionnées moi-même… elles sont pas trop PIMP mes cartes "blogdemaths" ?) : Pour une version imprimable (en pdf), cliquez ici: Cartes magiques. Mise en œuvre Voici comment se déroule le tour: (Remarque: Le fait d’écrire le nombre sur un papier n’est pas nécessaire mais il y a toujours des enf…. des plaisantins qui changeront de nombre à la fin et diront que ce n’est pas le nombre qu’ils avaient choisi juste pour nous prouver que notre tour ne marche pas… mais on ne blague pas avec les mathématiques.
Prise en main de GeoGebra 3D. Fenêtres 2D et 3D Au lancement de GGB, nous obtenons classiquement les deux fenêtres algèbre et graphique.
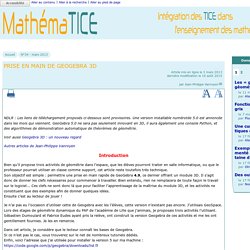
Ajoutons, à l’aide du menu Affichage, la fenêtre Graphique3D afin d’obtenir l’espace de travail suivant : Magie - Vie courante. Voici une manière fort simple de multiplier deux nombres (naturels).

On affirme que cette méthode est éthiopienne, égyptienne, caucasienne,... bref on ne sait pas trop d'où elle vient. Voyons comment on procède, en prenant un exemple. Soit à calculer le produit de 57 par 146. On tracera deux colonnes: la première commence par le premier facteur 57, la deuxième par le second facteur 146. Fabriquer le Tableau de Cent de Montessori : Modèle en Carton. Le Tableau de Cent, intégré à la pédagogie Montessori se présente sous la forme d’une planche permettant la manipulation et la visualisation dans le dénombrement de 0 à 100.
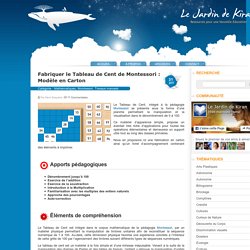
Ce matériel d’apparence simple, propose un éventail très riche d’applications pour toutes les opérations élémentaires et demeurera un support utile tout au long des classes primaires. Nous en proposons ici une fabrication en carton ainsi qu’un livret d’accompagnement contenant des éléments à imprimer. Apports pédagogiques Dénombrement jusqu’à 100Exercice de l’additionExercice de la soustractionIntroduction à la MultiplicationFamiliarisation avec les multiples des entiers naturelsApproche des pourcentagesAuto-correction. Réaliser la Table de Pythagore de Montessori : Modèle en Carton. Dans la continuité de notre article Réaliser une Planche de Multiplication Concrète : Modèle en Bois, nous abordons la table de Pythagore avec le modèle numérique tel qu’il a été décliné dans la pédagogie Montessori.
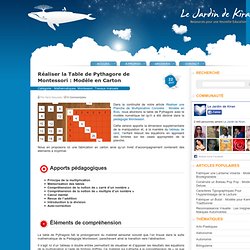
Cette version apporte la dimension supplémentaire de la manipulation et, à la manière du tableau de cent, l’enfant résoud les équations en apposant des timbres sur les cases appropriées de la planche. Nous en proposons ici une fabrication en carton ainsi qu’un livret d’accompagnement contenant des éléments à imprimer. Apports pédagogiques. Réaliser les Réglettes de Napier : Modèle en Carton. Sir John Napier of Merchiston est un mathématicien écossais plus connu pour le développement des premières tables logarithmiques au 17ème siècle.
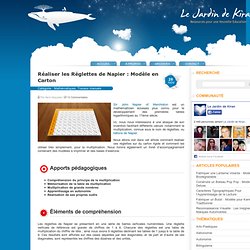
Ici, nous nous intéressons à une abaque de son invention facilitant différents calculs -notamment la multiplication, connue sous le nom de réglettes, ou bâtons de Napier. Nous allons voir dans cet article comment réaliser ces réglettes sur du carton rigide et comment les utiliser très simplement, pour la multiplication. L'extension Dmaths sur LibreOffice. I-A.
C'est quoi Dmaths▲ Dmaths est un logiciel ou (add-on) que l'on peut intégrer dans OpenOffice ou LibreOffice et qui génère des macros qui permettent d'éditer des formules scientifiques complexes et de faire des dessins variés. I-B. Pourquoi je l'utilise ! ▲ Je l'utilise pour enrichir et illustrer mes documents et mes devoirs, lorsque j'ai besoin d'écrire des formules ou de dessiner des figures complexes. Avant de commencer l'installation de Dmaths, il faut d'abord installer LibreOffice ou OpenOffice : Installation LibreOffice/OpenOffice.
XMaths - Cours et Exercices de Mathématiques. Comment les japonais apprennent à multiplier. Chinese Method of Multiplication (Lettuce Multiplication) L’Attrape Nombres. Cmath. Math'@ctivité 3D : flexagone. Le résultat final est un anneau de moebius à la façon d'Escher et il est manipulable.

Il se range dans une pochette d'origami lui servant de présentoir. Ce sont des objets en 3 dimensions (3D) même si le flexagone est applati lorsqu'il n'est pas manipulé. Pour voir le flexagone en action, cliquer sur l'animation ci-contre puis sur le bouton play. Pour voir une autre animation vidéo, cliquer sur l'icône suivante ("V" comme vidéo) puis 2 fois sur le bouton "play" : . Infos... Des fichiers d'impression 3D et de découpe automatique ou laser sont disponibles sur mon site à l'adresse : Dans nos classes - Les alignements, source de bien des jeux et défis ! - 15 décembre 2012 - Joëlle Lamon [1] Introduction Au cours du temps se sont développés de nombreux jeux et défis liés aux alignements de points : problèmes de plantations d’arbres, de réseaux de points, mais aussi morpion, puissance 4, … Nous en proposons ici une analyse.