

Creative Commons. Fraction comparison for 4th Graders.
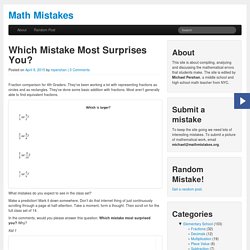
They’ve been working a lot with representing fractions as circles and as rectangles. They’ve done some basic addition with fractions. Before the iPhone, man had rocks.

The first true multi-tools were of course rocks. Take the chopper, a crude tool chipped from the volcanic stone nephelinite. First used in Tanzania some 1.85 million years ago, it was the stone-age equivalent of the smartphone. Grant me the imperfect comparison: For thousands of years, the chopper served most of humanity’s needs. It was used to hunt, to dig, to build and butcher.
Small Cubicuboctahedron – Robert Webb This is the small cubicuboctahedron, as drawn by Robert Webb’s Great Stella software.
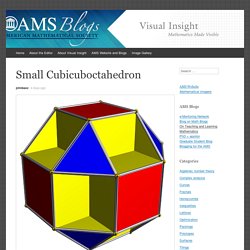
It looks simple enough, but it conceals some interesting mathematics. For starters, the yellow pieces are actually regular octagons which are mostly hidden from view.