

Medidas descriptivas. MedidasDescriptivas.pdf. Medidas descriptivas. Introducción El estudio de una variable estadística comienza con la obtención de datos, bien sondeando la población o tomando una muestra.

El siguiente paso en el proceso es la ordenación de datos elaborando la tabla correspondiente. Trabajar con una tabla es complejo y tedioso por lo que es más conveniente la introducción de nuevos parámetros que nos permitan resumir la información que contienen esas tablas. El objetivio que se persigue es la sintetización de la información que nos aportan los datos con la menor pérdida posible. Vamos a agrupar los parámetros en tres grupos dependiendo de su función.
MEDIDAS ESTADÍSTICAS DESCRIPTIVA. Medidas descriptivas. Procesamiento de la información: Tablas y Gráficos. Formas de recopilar, organizar, procesar e interpretar datos en tablas y gráficos Recopilar y procesar datos se ha convertido en una necesidad imperiosa en la actualidad.
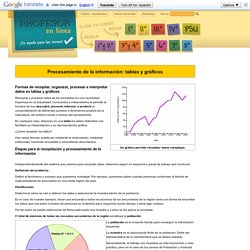
Conocerlos e interpretarlos le permite al hombre de hoy descubrir, prevenir, informar o predecir el comportamiento de diferentes sucesos o fenómenos propios de la naturaleza, del entorno social o incluso del pensamiento. En cualquier caso, disponer en una tabla los datos obtenidos nos facilitará su interpretación y su representación gráfica. ¿Cómo recopilar los datos? Hay varias formas: puede ser mediante la observación, mediante entrevistas, haciendo encuestas o consultando documentos.
Ejercicios De Representacion Grafica De La Informacion. Curso GRATIS de Estadistica. Aulafacil.com Estad�stica Descriptiva. Razonamiento Lógico Matemático. Tablas de frecuencia y gráficos. 1- ¿Para qué nos sirven los gráficos y las tablas de datos?
Los gráficos y las tablas representan e interpretan información procedente de diferentes fuentes, de forma clara, precisa y ordenada. Casi todo tipos de información puede organizarse en una tabla de datos y ser representada en algún tipo de gráfico. 1.1- Gráficos Los gráficos permiten visualizar la información contenida en las tablas de manera rápida y sencilla, demostrando con mayor claridad la relación que estos datos tienen entre sí.
Los más conocidos son: A- Gráficos de barras Son aquellos que emplean rectángulos (barras) que se colocan paralelamente. Para construir un gráfico de barras, debes dibujar un eje vertical y otro horizontal. Sma1_u3lecc20.pdf. Distribucion%20de%20frecuencias%20.pdf. REPRESENTACIONES. Desarrollo con un ejemplo : gasolina repostada en una gasolinera por 16 clientes :

5.- MEDIDAS DE VARIABILIDAD - Estadística Descriptiva en Edu. Las medidas de variabilidad nos informan sobre el grado de concentración o dispersión que presentan los datos respecto a su promedio.

Llamaremos homogénea, concentrada o poco dispersa a aquella distribución en la que todos los datos están cercanos al centro, como 4 4 5 5 5 5 6 6 6 6 7, y heterogénea o dispersa a la distribución con datos más separados del centro, como 1 3 5 8 10 16 20. Existen muchas formas de medir la variabilidad. Se Destacan las más importantes: MEDIDAS_%20DE_%20VARIABILIDAD.pdf. Medidas de tendencia central. La medidas de centralización nos indican en torno a qué valor (centro) se distribuyen los datos.
La medidas de centralización son: Moda La moda es el valor que tiene mayor frecuencia absoluta. Se representa por Mo. Se puede hallar la moda para variables cualitativas y cuantitativas. Hallar la moda de la distribución: 2, 3, 3, 4, 4, 4, 5, 5 Mo= 4 Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas. 1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9Mo= 1, 5, 9 Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes. 0, 1, 3, 3, 5, 5, 7, 8Mo = 4. Estadística: Medidas de tendencia central. Medidas de tendencia central: Media, Mediana, Moda Supóngase que un determinado alumno obtiene 35 puntos en una prueba de matemática.
Este puntaje, por sí mismo tiene muy poco significado a menos que podamos conocer el total de puntos que obtiene una persona promedio al participar en esa prueba, saber cuál es la calificación menor y mayor que se obtiene, y cuán variadas son esas calificaciones. En otras palabras, para que una calificación tenga significado hay que contar con elementos de referencia generalmente relacionados con ciertos criterios estadísticos. Las medidas de tendencia central (media, mediana y moda) sirven como puntos de referencia para interpretar las calificaciones que se obtienen en una prueba.
Volviendo a nuestro ejemplo, digamos que la calificación promedio en la prueba que hizo el alumno fue de 20 puntos. Medidas de tendencia central. Medidas de tendencia central (Localización) Contenido Media Aritmética La media aritmética de n observaciones de la variable X se denotará por el símbolo y se define como la suma de ellas dividida por n.

Simbólicamente: Medidas%20de%20tendencia%20Central.pdf. Medidas de variabilidad o dispersión. Los estadísticos de tendencia central o posición nos indican donde se sitúa un grupo de puntuaciones.

Los de variabilidad o dispersión nos indican si esas puntuaciones o valores están próximas entre sí o si por el contrario están o muy dispersas. Una medida razonable de la variabilidad podría ser la amplitud o rango, que se obtiene restando el valor más bajo de un conjunto de observaciones del valor más alto. Es fácil de calcular y sus unidades son las mismas que las de la variable, aunque posee varios inconvenientes: No utiliza todas las observaciones (sólo dos de ellas); Se puede ver muy afectada por alguna observación extrema; B.3) Medidas de Tendencia Central - Estadística.
Las medidas de tendencia central son valores que se ubican al centro de un conjunto de datos ordenados según su magnitud.

Generalmente se utilizan 4 de estos valores también conocidos como estadigrafos, la media aritmética, la mediana, la moda y al rango medio. Medidas de tendencia central. Ejercicios de medidas de tendencia central - HD. Untitled. Las medidas de posición dividen un conjunto de datos en grupos con el mismo número de individuos.
Para calcular las medidas de posición es necesario que los datos estén ordenados de menor a mayor. La medidas de posición son: Cuartiles Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales. Q1, Q2 y Q3 determinan los valores correspondientes al 25%, al 50% y al 75% de los datos. Tema 3 Medidas De Posición. Medidas de posición no centrales: Cuartiles, deciles y percentiles. Medidas de posicion. Medidas de posición Cuartiles Datos agrupado Datos no agrupados Deciles Percentiles y centiles Tanto las medidas de tendencia central como de dispersión en ocasiones son insuficientes sobre todo cuando en ocasiones deseamos presentar el análisis con respecto a la posición que ocupa la información que para nosotros resulta relevante, así por ejemplo, podemos hablar de dividir la información a la mitad, realizado por la mediana, en cuatro parte, en cinco, en diez o quizá en otro tipo de divisiones.
Parte2.pdf. NOCIONES DE PROBABILIDAD. Probabilidad y Estadistica. l1unida6.pdf. Nociones de probabilidad. Nociones de Probabilidad y Ejemplos. Capitulo 1 Probabilidad la regla de Laplace como el cociente entre el número de casos favorables a , y el de todoslos posibles resultados del experimento: Problemas resueltos de probabilidad. TA01062332005.pdf. Ejercicios Resueltos: Razonamiento Matemático.
1.- ¿Qué letra continua en la siguiente sucesión? Matematica1. PROBLEMA 300 : Se colocan 27 cubitos formando un solo cubo , y se pinta cada cara del cubo grande . El número de cubos que tiene 1 ; 2 y 3 caras pintadas en cada caso . A) 6 ; 12 y 8 B) 6 ; 10 y 6 C) 4 ; 10 y 8 D) 10 ; 6 y 2 E) 4 ; 12, 8 En los siguientes enlaces , dispondras de textos y videos de razonamiento lógico en pdf Cuántos árboles hay en un campo triangular que tiene un árbol en cada vértice y 5 en cada lado .
A) 15 B) 14 C) 13 D) 12 E) 10 En una bolsa hay pelotas, tres de ellas son rojas y dos son blancas . Sea A , B y C , tres lapiceros donde 2 de ellos son azules y uno es rojo , además A y B son de diferentes colores . Sean M , N y S canicas , donde dos son rojas y una es blanca . En una pareja de esposos que tiene 4 hijos varones , se sabe que cada hijo tiene una hermana . En una reunión se encuentra dos padres dos hijos y un nieto .
Razonamiento Matemático - Problemas Resueltos. Razonamiento geometrico. Razonamiento geometrico 107. Trigonometría. Trigonometría. Trigonometría. Definición de razones trigonométricas. Trigonometría es el nombre de la rama de la matemática que se dedica realizar cálculos vinculados a los elementos de un triángulo. Para esto trabaja con unidades como el grado sexagesimal (que se emplea al dividir una circunferencia en 360 grados sexagesimales), el grado centesimal (la división se realiza en 400 grados centesimales) y el radián (que se toma como la unidad natural de los ángulos y señala que la circunferencia es susceptible de división en 2 pi radianes). Razones Trigonométricas 01. Razones trigonométricas. Razones trigonométricas. Razones trigonométricas.
Razones trigonométricas en un triángulo rectángulo Seno El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa. Dg_clps_12.pdf. Ejercicios interactivos de razones trigonométricas. CP2VEST61QuestTrigonEspanhol.pdf. Ejercicios y problemas resueltos de trigonometría. Matematica1. OBJETIVOS : * Conocer correctamente las definiciones de las razones trigonométricas de un ángulo agudo. * Calcular las razones trigonométricas de un ángulo agudo a partir del triángulo rectángulo en que se encuentre. Una figura quizás poco conocida en algunos aspectos es la de Pitágoras, filósofo nacido en Samos hacia el siglo VI a.
C., gran matemático, autor de famosos legados: la tabla, el teorema y el triángulo, que llevan su nombre. Se cuenta que era muy hermoso, al extremo que sus discípulos lo comparan con Apolo andando sobre la Tierra. u3trigreto.pdf.