

Le concept de champ. Electromagnetic wave equation. Where.
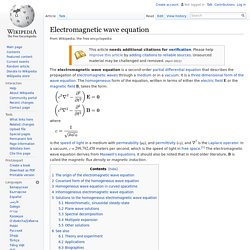
Electric field. Electric field lines emanating from a point positive electric charge suspended over an infinite sheet of conducting material.
Qualitative description[edit] An electric field that changes with time, such as due to the motion of charged particles producing the field, influences the local magnetic field. That is: the electric and magnetic fields are not separate phenomena; what one observer perceives as an electric field, another observer in a different frame of reference perceives as a mixture of electric and magnetic fields. For this reason, one speaks of "electromagnetism" or "electromagnetic fields". In quantum electrodynamics, disturbances in the electromagnetic fields are called photons. Magnetic flux. Inductors. John Hutchinson sur les ondes électromagnetique. A Dynamical Theory of the Electromagnetic Field. "A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865.[1] It is the paper in which the original set of four Maxwell's equations first appeared.
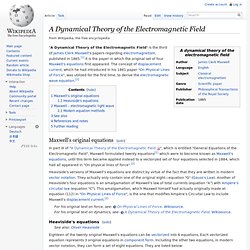
The concept of displacement current, which he had introduced in his 1861 paper "On Physical Lines of Force", was utilized for the first time, to derive the electromagnetic wave equation.[2] A Dynamical Theory of the Electromagnetic Field. 4'30 3/5 Cours d'EFT "l'inversion psychologique" Loi de Lenz-Faraday.
Un article de Wikipédia, l'encyclopédie libre.
La première. What's a Tensor? Electromagnetism - Part 2 - A Level Physics. 1. Course Introduction and Newtonian Mechanics. Maxwell's Equations. Fourier series, wikipedia. In mathematics, a Fourier series (English pronunciation: /ˈfɔərieɪ/) decomposes periodic functions or periodic signals into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or complex exponentials).
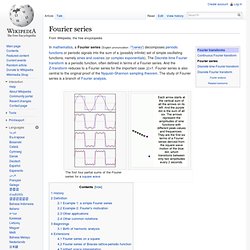
The Discrete-time Fourier transform is a periodic function, often defined in terms of a Fourier series. And the Z-transform reduces to a Fourier series for the important case |z|=1. Fourier series is also central to the original proof of the Nyquist–Shannon sampling theorem. The study of Fourier series is a branch of Fourier analysis. History[edit] The Fourier series is named in honour of Jean-Baptiste Joseph Fourier (1768–1830), who made important contributions to the study of trigonometric series, after preliminary investigations by Leonhard Euler, Jean le Rond d'Alembert, and Daniel Bernoulli. The heat equation is a partial differential equation. Definition[edit] is a periodic function with period P. Where: approximates on Other applications[edit] Dirac equation. In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928.
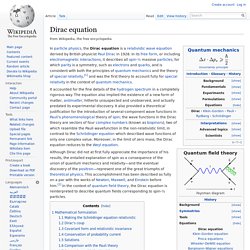
In its free form, or including electromagnetic interactions, it describes all spin-½ massive particles, for which parity is a symmetry, such as electrons and quarks, and is consistent with both the principles of quantum mechanics and the theory of special relativity,[1] and was the first theory to account fully for special relativity in the context of quantum mechanics. Although Dirac did not at first fully appreciate the importance of his results, the entailed explanation of spin as a consequence of the union of quantum mechanics and relativity—and the eventual discovery of the positron—represent one of the great triumphs of theoretical physics. Mathematical formulation[edit] The Dirac equation in the form originally proposed by Dirac is:[3] where ψ = ψ(x, t) is the wave function for the electron of rest mass m with spacetime coordinates x, t. 14. Maxwell's Equations and Electromagnetic Waves I.
Maxwell's equations. Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits.
These fields in turn underlie modern electrical and communications technologies. Maxwell's equations describe how electric and magnetic fields are generated and altered by each other and by charges and currents. They are named after the Scottish physicist and mathematician James Clerk Maxwell, who published an early form of those equations between 1861 and 1862. The equations have two major variants. The "microscopic" set of Maxwell's equations uses total charge and total current, including the complicated charges and currents in materials at the atomic scale; it has universal applicability but may be unfeasible to calculate. Maxwell's Equations - Basic derivation.
Electricity - A Level Physics. Electromagnetism - Part 1 - A Level Physics. Maxwell's Equations. Circular Motion - A Level Physics. Onde acoustique ionique. Un article de Wikipédia, l'encyclopédie libre.
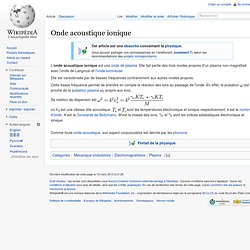
L'onde acoustique ionique est une onde de plasma. Elle fait partie des trois modes propres d'un plasma non-magnétisé avec l'onde de Langmuir et l'onde lumineuse. Elle est caractérisée par de basses fréquences contrairement aux autres modes propres. Cette basse fréquence permet de prendre en compte la réaction des ions au passage de l'onde. En effet, la pulsation est proche de la pulsation plasma propre aux ions. Sa relation de dispersion est où est une vitesse dite acoustique, et sont les températures électronique et ionique respectivement, k est le nombre d'onde, K est la Constante de Boltzmann, M est la masse des ions, sont les indices adiabatiques électronique et ionique. Comme toute onde acoustique, son aspect corpusculaire est décrite par les phonons. Portail de la physique. Cours #1 d'introduction à l'électromagnétisme (L2)