

Artista de teselaciones. ¡Las matemáticas y el arte se unen!
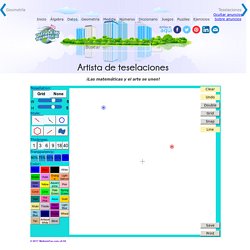
Tessellation: Style: Thickness: Transparency: Color: © 2017 MathsIsFun.com v0.92 Para empezar, ¡juega con él! Direcciones de teselación Puedes controlar el espacio entre losetas cambiando las direcciones de teselación. Ahora prueba distintos valores, pulsando "Teselar" después de cada cambio para ver el resultado. Polígonos Puedes dibujar polígonos regulares usando la herramienta de polígonos. Retoque y Deshacer Después de añadir una forma, puedes hacer un "Retoque" para ponerla en su sitio o ajustar su tamaño.
¿Qué puedes hacer? ¡Puedes dibujar todo tipo de patrones interesantes! Applet de Geogebra. #WorldTessellationDay #animation! Triangular → Square → Hexagonal → Triangular. Colour thanks to @g_benderski. #GeoGebra #Geometry #MathGif. 3/3 Octàgon irregular completat fins al dodecàgon regular amb patterns blocks.… General square-ish tilings! #mathart. 2/3 Tessel.lant amb patterns blocks… Feliz día de las teselaciones! #worldtessellationday. En Bucarest, nos podemos encontrar en sus aceras estas teselaciones: #worldtessellationday. ¿Organizamos un concurso de teselaciones del plano con temática de Terror ahora que viene Halloween? #TeselacionesTerroríficas. (II)Los maravillosos pavimentos geométricos del Templo Dorado en Amritsar, India. Matemáticas y Arte … Los maravillosos pavimentos geométricos del Templo Dorado en Amritsar, India. Matemáticas y Arte.
Actividades para trabajar los mosaicos de Escher - Aprendiendo matemáticas. Doble genialidad de @AkiyoshiKitaoka. El patrón está alineado tanto vertical como horizontalmente, y además el color central (el tono de gri… 1/3 Tessel.lant amb patterns blocks.… La geometria non euclidea. Hexágonos irregulares. MOSAICOS Y TESELADOS arte geometrico. Tema interesante si los hay para estudiar y construir figuras, para analizar Cubrimiento de superficiesRelaciones angularesMovimiento en el PlanoConstrucciones Geométricas.
Es el de construcción de mosaicos y teselados…..En este caso podemos construir mosaicos como los de la Alhambra, recurrir a un artista como Escher es uno de los más grandes ejemplos de como el arte y la matemática van emparejados Teselaciones, es un patrón repetitivo de figuras geométricas, de animales o humanas, que están intercaladas entre sí y no dejan espacios libres, es decir, están ordenadas de forma continua, sin superponerse. Se pueden hallar en los diseños ornamentales en pisos, paredes, alfombras, telas, grabados que conforman diversas figuras que podrían seguir de manera infinita, intrincada y precisa. Se requiere de matemáticas, de ciencia, pero sobre todo arte, pues se basa principalmente en el uso del hexágono –un polígono de seis lados y seis vértices. Esto deja tres opciones: los cuadrados (90º) pintar. Teselas de La Alhambra: Teselaciones Periódicas del Plano. Las calzadas romanas, tenían –entre otros- como objetivo el facilitar el paso de las personas, caravanas, animales, etc.
Por tanto, una de las características más importantes que debieran cumplir sería que no admitiesen huecos para así evitar caídas y lesiones tanto de personas como de animales, generalmente cargados; es decir, se trataba de cubrir por completo la calzada; es, en este sentido, en el que podemos decir que una calzada romana es uno de los primeros ejemplos de la historia de la teselación, pues como veremos ahora una teselación, grosso modo, no es más que un recubrimiento del plano que no deja resquicios. En la mitología griega las musas (en griego antiguo μοῦσαι mousai) eran, según los escritores más antiguos, las diosas inspiradoras de la música y, según las nociones posteriores, divinidades que presidían los diferentes tipos de poesía, así como las artes y las ciencias.
Museo Arqueológico de Nîmes, Francia. Segunda mitad del siglo I a. C. Cómo cubrir el plano con un mismo polígono (sin dejar huecos) □ De niños, todos hemos hecho garabatos en una clase aburrida, como mecanismo de defensa de nuestras neuronas, ante palabras vacías de contenido y emoción.
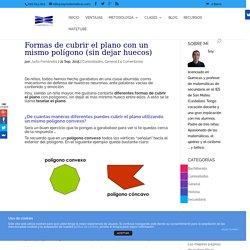
Hoy, siendo un niño mayor, me gustaría contarte diferentes formas de cubrir el plano con polígonos, sin dejar el más mínimo hueco entre ellos. A esto se le llama teselar el plano. ¿De cuántas maneras diferentes puedes cubrir el plano utilizando un mismo polígono convexo? Será un buen ejercicio que te pongas a garabatear para ver si te quedas cerca de la respuesta … Te recuerdo que en un polígono convexo todos los vértices “señalan” hacia el exterior del polígono.