Knapsack problem
Get flash to fully experience Pearltrees
Journal of Theoretical Biology : The promise of Mechanical Turk: How online labor markets can help theorists run behavioral experiments
Combining evolutionary models with behavioral experiments can generate powerful insights into the evolution of human behavior. The emergence of online labor markets such as Amazon Mechanical Turk (AMT) allows theorists to conduct behavioral experiments very quickly and cheaply.
Iowa Electronic Markets - Wikipedia, the free encyclopedia
Iowa Electronic Market for 2008 Democratic National Primary.
Prediction market - Wikipedia, the free encyclopedia
Prediction markets (also known as predictive markets , information markets , decision markets , idea futures , event derivatives , or virtual markets ) are speculative markets created for the purpose of making predictions. The current market prices can then be interpreted as predictions of the probability of the event or the expected value of the parameter.
Knapsack problem - Wikipedia, the free encyclopedia
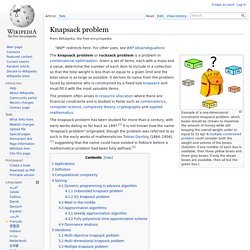
Example of a one-dimensional (constraint) knapsack problem: which boxes should be chosen to maximize the amount of money while still keeping the overall weight under or equal to 15 kg? A multiple constrained problem could consider both the weight and volume of the boxes.
Happiness
In mathematics and computer science , an optimization problem is the problem of finding the best solution from all feasible solutions . Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete.
Optimization problem - Wikipedia, the free encyclopedia
Complexity