Complexity
Get flash to fully experience Pearltrees
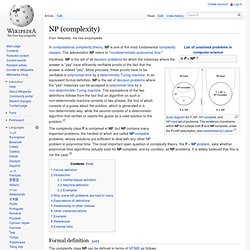
In computational complexity theory , NP is one of the most fundamental complexity classes . The abbreviation NP refers to " nondeterministic polynomial time ." Intuitively, NP is the set of all decision problems for which the instances where the answer is "yes" have efficiently verifiable proofs of the fact that the answer is indeed "yes".
NP (complexity)
Complexity class
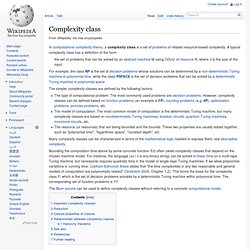
In computational complexity theory , a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form: the set of problems that can be solved by an abstract machine M using O (f( n )) of resource R, where n is the size of the input. For example, the class NP is the set of decision problems whose solutions can be determined by a non-deterministic Turing machine in polynomial time , while the class PSPACE is the set of decision problems that can be solved by a deterministic Turing machine in polynomial space . The simpler complexity classes are defined by the following factors:Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other. A computational problem is understood to be a task that is in principle amenable to being solved by a computer, which is equivalent to stating that the problem may be solved by mechanical application of mathematical steps. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used.
An abstract machine , also called an abstract computer , is a theoretical model of a computer hardware or software system used in automata theory . Abstraction of computing processes is used in both the computer science and computer engineering disciplines and usually assumes discrete time paradigm . [ edit ] Information In the theory of computation , abstract machines are often used in thought experiments regarding computability or to analyze the complexity of algorithms ( see computational complexity theory ).
Abstract machine