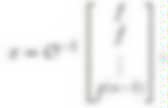
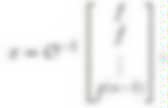
Peter J. Olver - Applied Mathematics. Peter J.

Olver Last Updated: January 4, 2014 Note: The first 11 chapters, including the exercises, are now published as a self-contained textbook, Applied Linear Algebra, coauthored with Chehrzad Shakiban. Most of chapters 11-15, 17, 18, and 22, including the exercises, are now incorporated in my new textbook, Introduction to Partial Differential Equations. Chapters Linear Algebraic Systems. George Cain - Complex Analysis. By George Cain (c)Copyright 1999, 2001 by George Cain.

All rights reserved. This is a textbook for an introductory course in complex analysis. It has been used for our undergraduate complex analysis course here at Georgia Tech and at a few other places that I know of. I owe a special debt of gratitude to Professor Matthias Beck who used the book in his class at SUNY Binghamton and found many errors and made many good suggestions for changes and additions to the book. Many thanks also to Professor Serban Raianu of California State University Dominguez Hills whose many helpful suggestions have considerably improved the book. I am also grateful to Professor Pawel Hitczenko of Drexel University, who prepared the nice supplement to Chapter 10 on applications of the Residue Theorem to real integration.
The notes are available as Adobe Acrobat documents. Title page and Table of Contents Table of Contents. Some Cryptography Theory. This is our Mathematics page with links to various topics we've written up.
We'll keep adding to this. Number theory: The multiplicative group modulo p Looks at the multiplicative group modulo p for a prime p which is used in public key cryptography using discrete logarithms. We consider some of the properties relevant to its use in cryptography and recap on some basic group theory. Number theory: Solving the discrete logarithm problem with bdcalc. Steiner Surfaces - IPFW. Definition Let p0, p1, p2, p3 be quadratic polynomials in two variables u, v.
This means they're of the form. Uncoiling the spiral: Maths and hallucinations. December 2009 You can read a more accessible version of this article here.
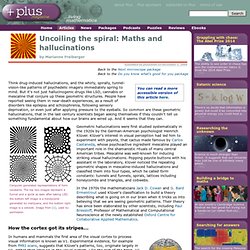
Think drug-induced hallucinations, and the whirly, spirally, tunnel-vision-like patterns of psychedelic imagery immediately spring to mind. But it's not just hallucinogenic drugs like LSD, cannabis or mescaline that conjure up these geometric structures. People have reported seeing them in near-death experiences, as a result of disorders like epilepsy and schizophrenia, following sensory deprivation, or even just after applying pressure to the eyeballs. So common are these geometric hallucinations, that in the last century scientists began asking themselves if they couldn't tell us something fundamental about how our brains are wired up.
Computer generated representations of form constants. Math and Programs you might be interested in. Math and Programs you might be interested in.
^That I found to be really intriguing. It's like not only did Turing invent the concept of the modern computer, but he also created math on paper that is remarkably similar to programmed shaders. ^^Context free. Very nice tool. Science After Sunclipse » Blog Archive » “Is Algebra Necessary?” Are You High? “This room smells of mathematics!
Go out and fetch a disinfectant spray!” —A.H. Trelawney Ross, Alan Turing’s form master. Offset curves. Miurafold.png (1602×945) Tupper's self-referential formula. Tupper's self-referential formula is a self-referential formula defined by Jeff Tupper that, when graphed in two dimensions, can visually reproduce the formula itself.
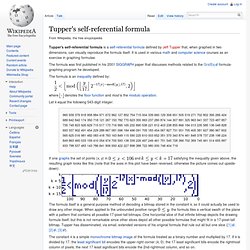
It is used in various math and computer science courses as an exercise in graphing formulae. The formula was first published in his 2001 SIGGRAPH paper that discusses methods related to the GrafEq formula-graphing program he developed. where denotes the floor function and mod is the modulo operation. Let k equal the following 543-digit integer: If one graphs the set of points (x, y) in and satisfying the inequality given above, the resulting graph looks like this (note that the axes in this plot have been reversed, otherwise the picture comes out upside-down): The formula itself is a general purpose method of decoding a bitmap stored in the constant k, so it could actually be used to draw any other image. A Programmer's Apology: The Library of Babel function. MathWorld calls this Tupper's Self-Referential Formula because a graph of that inequality in the domain 0<x<105, N<y<N+16 for a particular 541-digit number N shows an image of the function itself.
Closer investigation reveals that MathWorld does not even begin to do justice to the function, for higher up on the graph of this function one can find the complete works of Shakespeare, the contents of the lost library of Alexandria, and perhaps even the solution to unifying quantum mechanic with general relativity! At y values nearer the origin, you can find tomorrow's winning lottery number! If that sounds unbelievable, read on.... Consider rearranging the function slightly, as above, with k=17. Then note that in the domain used, N<y<N+k-1 the numerator, floor(y/k) is a constant. What is the value of the bit at position index in the binary representation of B?