

Hyperbolic geometry. Lines through a given point P and asymptotic to line R.
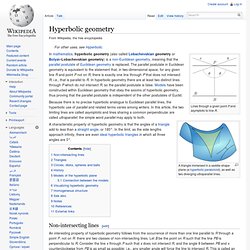
A triangle immersed in a saddle-shape plane (a hyperbolic paraboloid), as well as two diverging ultraparallel lines. In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced. The parallel postulate in Euclidean geometry is equivalent to the statement that, in two-dimensional space, for any given line R and point P not on R, there is exactly one line through P that does not intersect R; i.e., that is parallel to R. In hyperbolic geometry there are at least two distinct lines through P which do not intersect R, so the parallel postulate is false. Models have been constructed within Euclidean geometry that obey the axioms of hyperbolic geometry, thus proving that the parallel postulate is independent of the other postulates of Euclid.
Non-intersecting lines[edit] . Triangles[edit] . Using. Gyroid Surface. Voronoi diagram. 20 points and their Voronoi cells (larger version below).
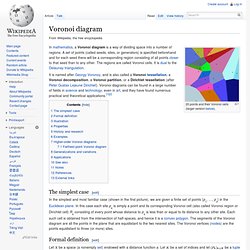
It is named after Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi diagrams can be found in a large number of fields in science and technology, even in art, and they have found numerous practical and theoretical applications.[1][2] The simplest case[edit] Formal definition[edit] Let . Gyroid. Gyroid A gyroid is an infinitely connected triply periodic minimal surface discovered by Alan Schoen in 1970.[1][2] History and Properties[edit] The gyroid is the unique non-trivial embedded member of the associate family of the Schwarz P and D surfaces with angle of association approximately 38.01°.
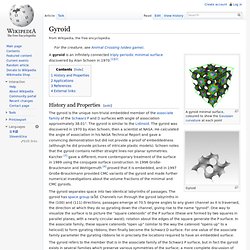
The gyroid is similar to the Lidinoid. The gyroid was discovered in 1970 by Alan Schoen, then a scientist at NASA. The gyroid separates space into two identical labyrinths of passages. Schwarz minimal surface. In differential geometry, the Schwarz minimal surfaces are periodic minimal surfaces originally described by Hermann Schwarz.
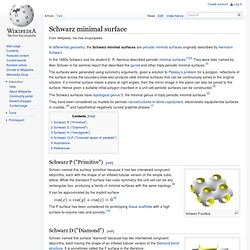
In the 1880s Schwarz and his student E. R. Lidinoid. Lidinoid in a unit cell.
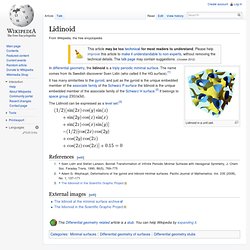
In differential geometry, the lidinoid is a triply periodic minimal surface. The name comes from its Swedish discoverer Sven Lidin (who called it the HG surface).[1] Gaussian curvature. In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point.
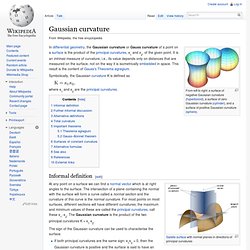
It is an intrinsic measure of curvature, i.e., its value depends only on distances that are measured on the surface, not on the way it is isometrically embedded in space. Minimal surface. Mean curvature. In mathematics, the mean curvature of a surface is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space.
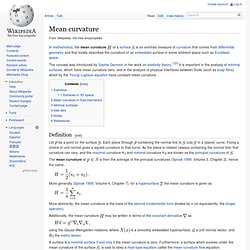
The concept was introduced by Sophie Germain in her work on elasticity theory.[1][2] It is important in the analysis of minimal surfaces, which have mean curvature zero, and in the analysis of physical interfaces between fluids (such as soap films) which by the Young–Laplace equation have constant mean curvature. Triply periodic minimal surface. Schwarz H surface These surfaces have the symmetries of a crystallographic group.
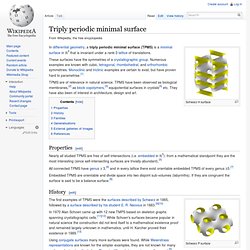
Numerous examples are known with cubic, tetragonal, rhombohedral, and orthorhombic symmetries. Monoclinic and triclinic examples are certain to exist, but have proven hard to parametrise.[1] TPMS are of relevance in natural science. TPMS have been observed as biological membranes,[2] as block copolymers,[3] equipotential surfaces in crystals[4] etc. Properties[edit] Nearly all studied TPMS are free of self-intersections (i.e. embedded in ℝ3): from a mathematical standpoint they are the most interesting (since self-intersecting surfaces are trivially abundant).[5] All connected TPMS have genus ≥ 3,[6] and in every lattice there exist orientable embedded TPMS of every genus ≥3.[7] Embedded TPMS are orientable and divide space into two disjoint sub-volumes (labyrinths). Hilbert Curve by henryseg on Shapeways. A 3-dimensional version of the Hilbert space filling curve.
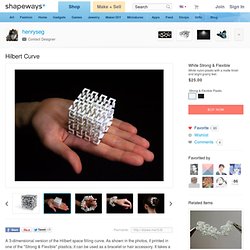
As shown in the photos, if printed in one of the "Strong & Flexible" plastics, it can be used as a bracelet or hair accessory. It takes a little time to reform back as a cube after being stretched, but it seems that leaving it overnight does the job. cm: 4.44 w x 4.44 d x 4.44 h in: 1.748 w x 1.748 d x 1.748 h. Andy Lomas homepage. Hilbert cube. In mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology.
Furthermore, many interesting topological spaces can be embedded in the Hilbert cube; that is, can be viewed as subspaces of the Hilbert cube (see below). Definition[edit] The Hilbert cube is homeomorphic to the product of countably infinitely many copies of the unit interval [0, 1]. In other words, it is topologically indistinguishable from the unit cube of countably infinite dimension. Gyroid. Marcus du Sautoy: Symmetry, reality's riddle. Marcus du Sautoy: «Las matemáticas explicarán el Universo como un gran sudoku»