

Identité d'Euler. Un article de Wikipédia, l'encyclopédie libre.
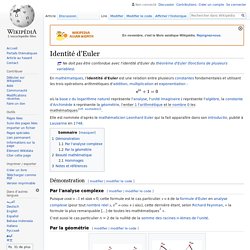
En mathématiques, l'identité d'Euler est une relation entre plusieurs constantes fondamentales et utilisant les trois opérations arithmétiques d'addition, multiplication et exponentiation : Elle est nommée d'après le mathématicien Leonhard Euler qui la fait apparaître dans son Introductio, publié à Lausanne en 1748.
Démonstration[modifier | modifier le code] Les nombres de Fibonacci - Kezako ? Complex numbers. This is an introduction to complex numbers.

It includes the mathematics and a little bit of history as well. It is intended for a general audience. The necessary background in a familiarity with ordinary real numbers (all positive and negative numbers and zero) and algebra. In one section some background in trigonometry is needed as indicated with the. Le Mystère Des Nombres Premiers. Nombres premiers. 1 : Conjecture sur les nombres premiers. 2 : Conjecture sur les nombres premiers. Nombres Clés. Nombre imaginaire pur. Un article de Wikipédia, l'encyclopédie libre.
Un nombre imaginaire pur est un nombre complexe qui s'écrit sous la forme ia avec a réel, i étant l'unité imaginaire. Par exemple, i, −i et 0 sont des imaginaires purs. Ce sont les nombres complexes dont la partie réelle est nulle. L'ensemble des imaginaires purs peut être noté iℝ (iR). Le carré d'un nombre imaginaire pur est un nombre réel négatif ou nul, et les racines carrées d'un nombre réel négatif sont des imaginaires purs. Définition[modifier | modifier le code] Dans le corps des nombres complexes on choisit un élément dont le carré vaut -1 que l'on note i.
La partie réelle de z est nulle ;z = - z (où z est le conjugué de z) ;z est nul ou bien son argument vaut π/2, modulo π ;Le nombre iz est un réel ;z2 est un nombre réel négatif. Les racines carrées d'un nombre réel sont soit réelles, quand ce nombre est positif, soit imaginaires pures quand ce nombre est négatif. Axe des imaginaires purs[modifier | modifier le code] Nombre complexe. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir complexe. L'ensemble des sommes et produits de nombres réels et du nombre imaginaire i (les nombres de la forme a + ib) (en électricité et en électronique, les nombres imaginaires sont identifiés par la lettre j au lieu de i, i étant en électricité et électronique l'intensité du courant) satisfait les propriétés d'une structure de corps commutatif qui contient le corps des réels. Il est appelé corps des nombres complexes et se note ℂ. Il est muni de l'application module qui généralise la valeur absolue des nombres réels, mais ne peut pas être ordonné totalement de façon compatible avec sa structure de corps. En algèbre, le théorème de d'Alembert-Gauss identifie le degré d'un polynôme complexe non nul au nombre de ses racines comptées avec leur ordre de multiplicité. En analyse, l'exponentielle complexe permet de simplifier l'étude des séries de Fourier, puis de définir la transformée de Fourier. Et . Le plan. Scienza_e_tecnologia » Russo dimostra teorema di Fermat tre righe per risolvere il rompicapo.
ROMA - Il Grande Teorema di Fermat, detto anche l'Ultimo teorema, ha ora una nuova dimostrazione.
A trovare la soluzione al rompicapo che da quattro secoli assilla matematici e ricercatori, è stato uno studioso russo, Aleksandr Ilin. Che ha annunciato di essere in grado di dimostrare questo famoso teorema. La dimostrazione è stata pubblicata oggi dal periodico moscovita "Novaya Gazeta". Ilin è professore di matematica applicata all'università di Omsk (Siberia occidentale) ed esperto di balistica. In base alle regole della comunità scientifica internazionale - sottolinea il periodico - la dimostrazione potrà essere considerata probante solo due anni dopo la pubblicazione, se in questo lasso di tempo nessuno riuscirà a confutarla. In precedenza altri studiosi avevano affermato di aver trovato la soluzione. Ma la sua odissea matematica non era ancora finita. Ultimo teorema di Fermat. Da Wikipedia, l'enciclopedia libera.
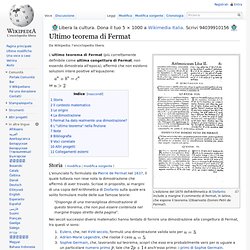
L'edizione del 1670 dell'Arithmetica di Diofanto include a margine il commento di Fermat, in latino, che espone il teorema (Observatio Domini Petri de Fermat). L'ultimo teorema di Fermat (più correttamente definibile come ultima congettura di Fermat, non essendo dimostrata all'epoca), affermò che non esistono soluzioni intere positive all'equazione: se Storia[modifica | modifica sorgente] L'enunciato fu formulato da Pierre de Fermat nel 1637, il quale tuttavia non rese nota la dimostrazione che affermò di aver trovato. "Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina".
Nei secoli successivi diversi matematici hanno tentato di fornire una dimostrazione alla congettura di Fermat, tra questi vi sono: La soluzione di Wiles fu pubblicata nel 1995 e premiata il 27 giugno 1997 con il Premio Wolfskehl, consistente in una borsa di 50 000 dollari.