

Unit type. The unit type is the terminal object in the category of types and typed functions.
It should not be confused with the zero or bottom type, which allows no values and is the initial object in this category. The unit type is implemented in most functional programming languages. The void type that is used in some imperative programming languages serves some of its functions, but because its carrier set is empty, it has some limitations (as detailed below). Top type. The top type in the type theory of mathematics, logic, and computer science, commonly abbreviated as top or by the down tack symbol (⊤), is the universal type, sometimes called the universal supertype as all other types in any given type system are subtypes of top.
Haskell/Denotational semantics. Introduction[edit] This chapter explains how to formalize the meaning of Haskell programs, the denotational semantics.
It may seem to be nit-picking to formally specify that the program square x = x*x means the same as the mathematical square function that maps each number to its square, but what about the meaning of a program like f x = f (x+1) that loops forever? In the following, we will exemplify the approach first taken by Scott and Strachey to this question and obtain a foundation to reason about the correctness of functional programs in general and recursive definitions in particular.
Of course, we will concentrate on those topics needed to understand Haskell programs.[1] Another aim of this chapter is to illustrate the notions strict and lazy that capture the idea that a function needs or needs not to evaluate its argument. What are Denotational Semantics and what are they for? Bottom type. In type theory, a theory within mathematical logic, the bottom type is the type that has no values.
It is also called the zero or empty type, and is sometimes denoted with falsum (⊥). A function whose return type is bottom cannot return any value. In the Curry–Howard correspondence, the bottom type corresponds to falsity. Brouwer–Heyting–Kolmogorov interpretation. In mathematical logic, the Brouwer–Heyting–Kolmogorov interpretation, or BHK interpretation, of intuitionistic logic was proposed by L.
E. J. Brouwer, Arend Heyting and independently by Andrey Kolmogorov. It is also sometimes called the realizability interpretation, because of the connection with the realizability theory of Stephen Kleene. The interpretation[edit] Type system. Dependent type. Dependent types add complexity to a type system.
Deciding the equality of dependent types in a program may require computations. If arbitrary values are allowed in dependent types, then deciding type equality may involve deciding whether two arbitrary programs produce the same result; hence type checking may become undecidable. History[edit] Dependent types were created to deepen the connection between programming and logic. In 1934, Haskell Curry noticed that the types used in mathematical programming languages followed the same pattern as axioms in propositional logic. Predicate logic is an extension of propositional logic, adding quantifiers. Type theory. In mathematics, logic, and computer science, a type theory is any of a class of formal systems, some of which can serve as alternatives to set theory as a foundation for all mathematics.
In type theory, every "term" has a "type" and operations are restricted to terms of a certain type. Two well-known type theories that can serve as mathematical foundations are Alonzo Church's typed λ-calculus and Per Martin-Löf's intuitionistic type theory. Type class. In computer science, a type class is a type system construct that supports ad hoc polymorphism.
This is achieved by adding constraints to type variables in parametrically polymorphic types. Such a constraint typically involves a type class T and a type variable a, and means that a can only be instantiated to a type whose members support the overloaded operations associated with T. Since their creation, many other applications of type classes have been discovered. Overview[edit] The programmer defines a type class by specifying a set of function or constant names, together with their respective types, that must exist for every type that belongs to the class. Polymorphism (computer science) Ad hoc polymorphism: when a function denotes different and potentially heterogeneous implementations depending on a limited range of individually specified types and combinations.
Ad hoc polymorphism is supported in many languages using function overloading.Parametric polymorphism: when code is written without mention of any specific type and thus can be used transparently with any number of new types. In the object-oriented programming community, this is often known as generics or generic programming. In the functional programming community, this is often simply called polymorphism.Subtyping (also called subtype polymorphism or inclusion polymorphism): when a name denotes instances of many different classes related by some common superclass.[3] In the object-oriented programming community, this is often simply referred to as polymorphism. Data type. This article is about data types in computer science and programming.
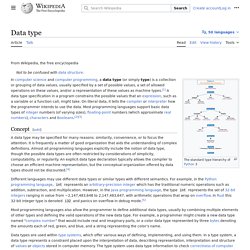
For their use in statistics, see statistical data type. In computer science and computer programming, a data type or simply type is a classification identifying one of various types of data, such as real, integer or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of that type can be stored.[1][2] Overview[edit] Data types are used within type systems, which offer various ways of defining, implementing and using them.
Type safety. Recursive data type. In computer programming languages, a recursive data type (also known as a recursively-defined, inductively-defined or inductive data type) is a data type for values that may contain other values of the same type. Data of recursive types are usually viewed as directed graphs. An important application of recursion in computer science is in defining dynamic data structures such as Lists and Trees. Recursive data structures can dynamically grow to a theoretically infinite size in response to runtime requirements; in contrast, a static array's size requirements must be set at compile time. Algebraic data type. The values of a sum type are typically grouped into several classes, called variants.
A value of a variant type is usually created with a quasi-functional entity called a constructor. Each variant has its own constructor, which takes a specified number of arguments with specified types. The set of all possible values of a sum type is the set-theoretical sum, i.e. the disjoint union, of the sets of all possible values of its variants.
Type constructor. In the area of mathematical logic and computer science known as type theory, a type constructor is a feature of a typed formal language that builds new types from old. Typical type constructors encountered are product types, function types, power types and list types. Simply typed lambda calculus. The simply typed lambda calculus ( Typed lambda calculus. ) to denote anonymous function abstraction. Curry–Howard correspondence. A proof written as a functional program: the proof of commutativity of addition on natural numbers in the proof assistant Coq. nat_ind stands for mathematical induction, eq_ind for substitution of equals and f_equal for taking the same function on both sides of the equality. Earlier theorems are referenced showing m = m + 0 and S (m + y) = m + S y.
In programming language theory and proof theory, the Curry–Howard correspondence (also known as the Curry–Howard isomorphism or equivalence, or the proofs-as-programs and propositions- or formulae-as-types interpretation) is the direct relationship between computer programs and mathematical proofs. Origin, scope, and consequences[edit] At the very beginning, the Curry–Howard correspondence is If one now abstracts on the peculiarities of this or that formalism, the immediate generalization is the following claim: a proof is a program, the formula it proves is a type for the program. The Curry-Howard Correspondence in Haskell. Tim Newsham. Correspondance de Curry-Howard. Un article de Wikipédia, l'encyclopédie libre. La correspondance de Curry-Howard, appelée[1] également isomorphisme de Curry-de Bruijn-Howard, correspondance preuve/programme ou correspondance formule/type, est une série de résultats à la frontière entre la logique mathématique, l'informatique théorique et la théorie de la calculabilité établissant une relation entre les démonstrations formelles d'un système logique et les programmes d'un modèle de calcul.
Les premiers exemples de correspondance de Curry-Howard remontent à 1958 date à laquelle Haskell Curry remarqua l'analogie formelle entre les démonstrations des systèmes à la Hilbert et la logique combinatoire, puis à 1969 où William Alvin Howard remarqua que les démonstrations en déduction naturelle intuitionniste pouvaient formellement se voir comme des termes du lambda-calcul typé. Historique[modifier | modifier le code] Logique implicative minimale[modifier | modifier le code] Intuitionistic type theory.