

Dimensions Chapter 7 and 8. Recall the formula which expresses the Hopf projection.
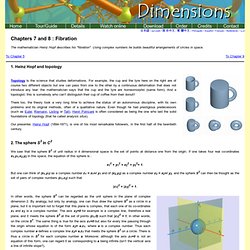
In terms of the complex co-ordinates, it sends (z1,z2) to the point a considered as a point of S2. Fixing a line of latitude p in S2, is the same as fixing the modulus of a complex number, so the pre-image of a line of latitude is described by an equation of the form |z2/z1| = constant. For example, let us choose 1 for this constant so that z1 and z2 have the same modulus. But don’t forget that |z1|2 + |z2|2 = 1, so the modulus of z1 and of z2 are both equal to √2/2. When we stereographically project this torus into 3 dimensional space from the North Pole, with co-ordinates (0,1), it isn’t difficult to verify that the projection of the torus is not only homeomorphic to a torus but it is actually a torus of revolution. MyToE » Search Results: 5040. A long and technical post to document a New Years Day (early morning) 2013 discovery!
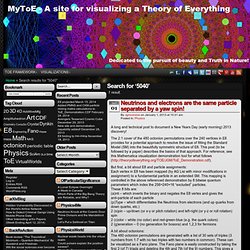
The 2:1 cover of the 480 octonion permutations over the 240 vertices in E8 provides for a potential approach to resolve the issue of fitting the Standard Model (SM) into the beautifully symmetric structure of E8. This post (to be followed by a paper) describes the basics of that approach. For reference, see this Mathematica visualization demonstration tool for what follows ( But first, a bit about E8 and particle assignments: Each vertex in E8 has been mapped (by AG Lisi with minor modifications in assignment) to a fundamental particle in an extended SM. This mapping is controlled in the above referenced demonstration by 8 bitwise quantum parameters which index the 256=240+16 “excluded” particles. A bit about octonions: The 480 octonion permutations are generated with a list of 30 sets of triples (3 numbers from 1-7 with no two triples with two numbers in common).
Hypercubes, Hexagons, Halayudha, Hermes, and Plato. Clifford Modules. John Baez had a weblog long before the term was even invented, and for many years now has been consistently putting out interesting current material about math and physics under the title This Week’s Finds in Mathematical Physics.
The latest edition has a beautiful explanation of the structure of modules of the Clifford algebra. Traditionally one thinks about geometry in n-dimensions in terms of n-dimensional vectors and tensors built by taking tensor products of vectors. These are all representations of the general linear group GL(n), or if one has a metric, the othogonal group SO(n) of transformations that preserve the metric. However, it turns out that there are representations more fundamental than vectors, the spinor representations. These require a metric for their definition, and are projective representations of SO(n), or true representations of the double-cover Spin(n). Www.maths.ed.ac.uk/~aar/slides/singexot.pdf. Www.nilesjohnson.net/hopf-articles/Lyons_Elem-intro-Hopf-fibration.pdf.
Orbifold construction of the modes of the Poincare dodecahedral space - Jeffrey Weeks. Platonic. If you have a slow internet connection try this version instead.

John Baez November 12, 2006 What's the pattern in this sequence? Infinity, five, six, three, three, three, three, three, ... Platonic Ratio. Numbers Magick. “The laws of nature are but the mathematical thoughts of God.” — Euclid The ancients claimed that God works by mathematics.
Their religion was a conglomeration of religion, astrology, alchemy, physical and mental science, and mathematics. Ancient astrology divided the starry heavens into 36 constellations. These were represented by different amulets called “Sigilla Solis,” or the sun seal. These amulets were worn by the pagan priests, and they contained all the numbers from 1 to 36 – Roy Allan Anderson, “Unfolding the Revelation” God Works by Numbers Science, and particularly geometry and astronomy, was linked directly to the divine for ancient builders of temples and monuments. God as Architect/Builder/Geometer/Craftsman, Codex Vindobonensis 2554 (French, ca. 1250), in the Österreichische Nationalbibliothek., The Frontispiece of Bible Moralisee. Platonic Solid Study #4: Dodecahedron. Understanding the geometry of dodecahedron.
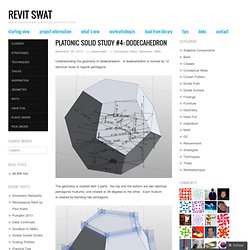
A dodecahedron is formed by 12 identical faces of regular pentagons. The geometry is created with 3 parts: the top and the bottom are two identical pentagonal frustums, one rotated at 36 degrees to the other. Each frustum is created by blending two pentagons. The middle part is a blend of two pentagons, one rotated at 36 degrees to the other. While blending the two pentagons, warp surfaces will be created instead of flat ones. Parameters and Math Like this: Like Loading...
The Kabbalah and Freemasonry. Prometheus Phoenix.