

Change-of-basis matrices I: Theory. 3D projection. 3D projection is any method of mapping three-dimensional points to a two-dimensional plane.
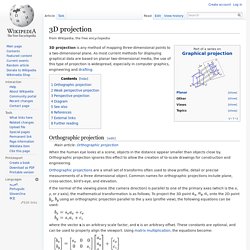
As most current methods for displaying graphical data are based on planar two-dimensional media, the use of this type of projection is widespread, especially in computer graphics, engineering and drafting. Orthographic projection[edit] When the human eye looks at a scene, objects in the distance appear smaller than objects close by. Orthographic projection ignores this effect to allow the creation of to-scale drawings for construction and engineering. Orthographic projections are a small set of transforms often used to show profile, detail or precise measurements of a three dimensional object.
If the normal of the viewing plane (the camera direction) is parallel to one of the primary axes (which is the x, y, or z axis), the mathematical transformation is as follows; To project the 3D point onto the 2D point where the vector s is an arbitrary scale factor, and c is an arbitrary offset. When and from. Android - How to calculate a specific distance inside of a picture? RunUpdateScript Command. Tutorial:Introduction to GeoGebraScript. Sometimes the ways students can interact with your worksheets using the basic features provided by GeoGebra are not powerful enough or too difficult to be used by your students, especially younger ones.
GeoGebraScript is there to help you creating simple-to-use constructions with more sophisticated interactivity. It is a simple way to write scripts (small programs) in GeoGebra. Common uses of scripting are: Checking student's answers by letting them enter their answers into textfields and using scripts to check if they are correct. Creating new tasks / challenges after the student pressed a button, either randomly generated or using a set of challenges defined by you. Starting animations or revealing new parts of the construction after the student pressed a button or finished his task.
Background: Commands There are not only tools to create an object in GeoGebra. Example: With the command Circle[(1,2),3] you'll get a circle with the center at (1,2) with a radius 3. Tutorial:Inserting Static and Dynamic Text into the GeoGebra’s Graphics View. Coordinates of Reflected Points Preparations Open a new GeoGebra window.
Switch to Perspectives - Algebra & Graphics and show the grid (View Menu). In the Options Menu set the Point capturing to Fixed to Grid. Construction Steps Inserting Text into the Graphics View Inserting static text. Tutorial:Scripting:Functions and subroutines. Tutorial: Functions and subroutines in Geogebra scripting Subroutines (also known as functions or procedures) are an important concept in computer programming, and help with program maintenance and code re-use.
This tutorial describes some ways that you can enjoy some of the advantages of subroutines in GeoGebra. Method 1. Custom tools act like a new function. They can take inputs and produce output objects as a result. Method 2. Method 3. Here's a more detailed example. Instead, let's use a subroutine. Target = "A" in the input bar. Next create a button called myButton. WildLinAlg1: Introduction to Linear Algebra (N J Wildberger) Linear Algebra. Math, Better Explained eBook + Video Course. Frustrated With Unhelpful, Mechanical Explanations?
I was too. I've spent years looking for the intuition behind the math concepts that seem to appear in every class, whether exponents or the Pythagorean Theorem. Slowly, over a decade, I've condensed the key insights (and the analogies that explain them) into friendly, clear, easy-to-read lessons. I want you to enjoy the Aha! Moments in math, moving beyond memorization to experiencing an idea firsthand. “Most of the fundamental ideas of science are essentially simple, and may, as a rule, be expressed in language comprehensible to everyone.” — Albert Einstein What You Will Learn. An Intuitive Guide to Linear Algebra. Despite two linear algebra classes, my knowledge consisted of “Matrices, determinants, eigen something something”.
Why? Well, let’s try this course format: Name the course Linear Algebra but focus on things called matrices and vectorsTeach concepts like Row/Column order with mnemonics instead of explaining the reasoningFavor abstract examples (2d vectors! 3d vectors!) And avoid real-world topics until the final week The survivors are physicists, graphics programmers and other masochists. Linear algebra gives you mini-spreadsheets for your math equations. Linear algebra. Linear algebra is the branch of mathematics concerning vector spaces and linear mappings between such spaces.
It includes the study of lines, planes, and subspaces, but is also concerned with properties common to all vector spaces. Linear algebra is central to both pure and applied mathematics. For instance, abstract algebra arises by relaxing the axioms of a vector space, leading to a number of generalizations. Functional analysis studies the infinite-dimensional version of the theory of vector spaces. Combined with calculus, linear algebra facilitates the solution of linear systems of differential equations. Techniques from linear algebra are also used in analytic geometry, engineering, physics, natural sciences, computer science, computer animation, and the social sciences (particularly in economics).
History[edit] Quickset for Windows 7 64-bit on XPS M170.