

Algorithmic worlds - 20040107-1. Various periodic tiles. The follows are notes on various tilings on the plane.

Written by Paul Bourke December 2001 Written by Paul Bourke June 2006 Named after Sebastien Truchet (1657 - 1729) who studied tiling of squares with a diagonal orientation. 2 Dimensions Single cell 2x2 tilings Each unit is randomly rotated by 0 or 90 degrees or flipped vertically or horizontally, there are only two unit states. 5x5 tilings Larger tiling [POVRay source] Orb.blue. Postwork - Mandelbulb3D with Parameter + Map by matze2001 on DeviantArt. Postwork - Mandelbulb3D with Parameter + Map by matze2001 on DeviantArt.
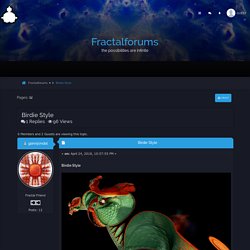
Postwork - Mandelbulb3D with Parameter + Map by matze2001 on DeviantArt. Birdie Style in Fractal Image Gallery - Page 1 of 1. Birdie Style This is one more outcome using the new 3D Newton introduced at MB3D v199 [JIT_gnj_RealPowNewton_04 , _RotatedFolding]
(Other) my concept art is based on fractal manipulations in Fractal Image Gallery - Page 1 of 3. Vanlindt Marc - Graphisme et Photographie. VANLINDT Marc. Charles Gilchrist. Artforms of Nature. Published on 18 July 2009 Haekel's artistic interpretation of the biological forms he studied have a clarity of symmetry and detail that has been a source of inspiration for many artists and engineers over the years.
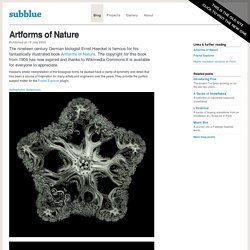
They provide the perfect subject matter for the Fractal Explorer plugin. Astrophyton darwinium: Kunstformen der Natur. Introduction[edit] The following images are plates, in order of their plate number from German biologist and illustrator Ernst Haeckel's Kunstformen der Natur (Artforms of Nature) (1904). 2.
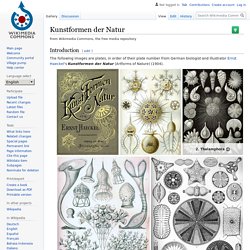
Thalamphora 8. Discomedusae 37. Siphonophorae 42. 100. Artforms of Nature. Distance Estimated 3D Fractals (Part I) During the last two years, the 3D fractal field has undergone a small revolution: the Mandelbulb (2009), the Mandelbox (2010), The Kaleidoscopic IFS’s (2010), and a myriad of equally or even more interesting hybrid systems, such as Spudsville (2010) or the Kleinian systems (2011).

All of these systems were made possible using a technique known as Distance Estimation and they all originate from the Fractal Forums community. Part I briefly introduces the history of distance estimated fractals, and discuss how a distance estimator can be used for ray marching. Part II discuss how to find surface normals, and how to light and color fractals. Part III discuss how to actually create a distance estimator, starting with distance fields for simple geometric objects, and talking about instancing, combining fields (union, intersections, and differences), and finally talks about folding and conformal transformation, ending up with a simple fractal distance estimator. The background. Sandin raytracerjuliasetsbw. Flash-pbk-collection/QuaternionJulia.pbk at master · vpmedia/flash-pbk-collection. Fractals, computer graphics, mathematics, demoscene and more.
Intro It's very usual to people to know that for the classic Mandelbrot set the period two hyperbolic component is a disc of radius 1/4 centered at -1.
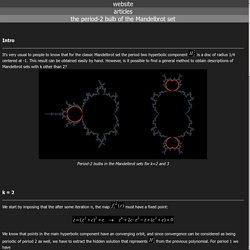
This result can be obtained easily by hand. Patterns of nature. Since the days of Da Vinci, art and science have always gone hand-in-hand, but it in the modern world there seems to be something of an intractable divide between the two.
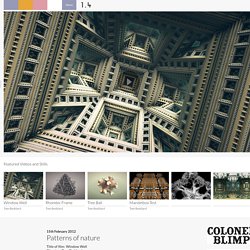
Cue renaissance man Tom Beddard (aka subBlue), a physicist-turned-filmmaker who uses his understanding of the algorithms and programming to create entrancing animations which echo the fractal patterns of nature. Laura Swinton reports As I understand it, your background is in physics. What inspired you to move into animation and filmmaking? I originally did a PhD in laser physics, however that was around the time of the first dot com boom which I wanted to be a part of. Developing material for the web requires a nice combination of creative and technical skills, something which appealed to me.
Perception by Swoopswatkill on DeviantArt. In a Wooden Place by Swoopswatkill on DeviantArt. Details of Decay by Swoopswatkill on DeviantArt. Change is Hard by Swoopswatkill on DeviantArt. Girard Desargues. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes »(décembre 2011).
Améliorez sa vérifiabilité en les associant par des références à l'aide d'appels de notes. Biographie[modifier | modifier le code] Mathématiques » Géométrie. Géométrie affine. Un article de Wikipédia, l'encyclopédie libre.
Dissocier les notions propres à la géométrie affine est récent dans l'histoire des mathématiques. La définition formelle actuelle d'un espace affine présuppose la donnée d'un espace vectoriel, appelé l'espace directeur. Deux points d'un espace affine peuvent se soustraire pour donner un vecteur de l'espace directeur. Parmi les résultats remarquables de la géométrie affine, on peut citer : Géométrie projective. Considérations historiques[modifier | modifier le code] Géométrie projective. Géométrie projective. Alexander polynomial. In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type.
James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984.
Chain complex. A cochain complex is similar to a chain complex, except that its homomorphisms follow a different convention. The homology of a cochain complex is called its cohomology. In algebraic topology, the singular chain complex of a topological space X is constructed using continuous maps from a simplex to X, and the homomorphisms of the chain complex capture how these maps restrict to the boundary of the simplex. The homology of this chain complex is called the singular homology of X, and is a commonly used invariant of a topological space.
Chain complexes are studied in homological algebra, but are used in several areas of mathematics, including abstract algebra, Galois theory, differential geometry and algebraic geometry. Algebraic topology. A torus, one of the most frequently studied objects in algebraic topology Although algebraic topology primarily uses algebra to study topological problems, using topology to solve algebraic problems is sometimes also possible. Algebraic topology, for example, allows for a convenient proof that any subgroup of a free group is again a free group. Patterns of Visual Math - 3 Dimensional Fractals & Mandelbulb. 3 Dimensional Fractals and the Search for the 'true' 3D Mandelbrot Three Dimensional Fractal Mappings Years ago, many fractal enthusiasts viewed these intricate and majestic patterns and thought "Wouldn't this be incredible in 3-D? ". Dozens of methods have been developed to view fractals in an arbitrary number of dimensions.
Quaternions are 3D shadows of 4D Julia Sets, which, if sliced in a plane, reveal the corresponding 2 dimensional Julia Set. Other attractive developments include 'Quasi-Fuchian" fractals and the recent popularity of the 'Mandelbulb" 3D Mandelbrot - which was exclusively discovered and implemented collaboratively by the inquisitive genius folks at Fractalforums.com. The palace of infinite wisdom and utter joy by elminino on DeviantArt. Cave - Mandelbulb3D with Parameter by matze2001 on DeviantArt. Terrain.party. Mandalay morning by elminino on DeviantArt. The Mandalay Trail by elminino on DeviantArt. Babel's City by elminino on DeviantArt. Behind the window - MB3D with Parameter by matze2001 on DeviantArt. Beginnings and ends by elminino on DeviantArt. Arcos y escaleras by elminino on DeviantArt.
Interior catedralicio by elminino on DeviantArt. Postwork - Mandelbulb3D with Parameter + Map by matze2001 on DeviantArt. Tilt-shift dIFS by elminino on DeviantArt. Mathias Mohr. Formula MandalayKIFS - Tips by LukasFractalizator on DeviantArt. Convert a Distance Estimate to a Mesh. Let me try that again. The 10s millions of polys is a problem. Short of waiting a couple of years for technology to catch up, you might consider starting with a low res mesh and use feature extraction for the interesting parts.
A lot of work has been done in the medical imaging field on this problem. A simple and direct approach is a 3D paint algorithm. The 3D paint algorithm will automatically grab only connected regions. 3D paint is not to complicated. The painter starts in a cube that is cut by the iso-surface. This is an ideal application for recursion because the to_do_list and scheduled_or_done is handled on the stack by the magic of the stack programming model. // add the starting point to the to_do_list and mark scheduled_or_done.to_do_list.add(start_cube);scheduled_or_done.add(start_cube); // Do the painting job.
The to_do_list object is a FIFO with add and next functions. Distance Estimated 3D Fractals (VI): The Mandelbox. MESMERIZING , INTRICATE AND EXQUISITE ARCHITECTURE OF QOM BUILDINGS. CITA PhD thesis - Jacob Riiber 2013 - Generative Processes in Architectural Design by CITA. What class of fractal - Mandelbox. To know what class of fractal a mandelbox is, we need to know the basic classes of 3d fractals. Since I can't find such a classification online, I have built my own classification based on the symmetric fractals of a 3x3x3 cube (see here). These give 81 types that can be reduced to a table of seven class names: As you can see, the Void fractals (first column) have no volume, and the solid fractals (bottom row) have no volume of space between the solid, so is hard to visualise, but the solid fractals are just a solid with internal borders (cracks) in the shape of the diagonally opposite void fractal.
The names 'tree' and 'sponge' should sound fairly standard, and 'cluster' is a good name I think (e.g. a star cluster). Mandelbox370. \( \newcommand{\iter}[2]{{#1}^{[#2]}} \newcommand{\mboxset}{M_{n,\mu}} \newcommand{\jboxset}[1]{J_{n,\mu, #1}} \newcommand{\itfnv}{T_{\mu,\vec{v}}} \newcommand{\itfnc}{T_{\mu,\vec{c}}} \newcommand{\itfnx}{T_{\mu,x_0}} \newcommand{\bfold}{F_{box}} \newcommand{\sfold}{F_{ball}} \newcommand{\implies}{\Rightarrow} \newcommand{\orbit}[1]{\left\{ \iter{#1}{n} \right\}} \newcommand{\setR}{\mathbb{R}} \newcommand{\norm}[1]{\|#1\|} \) The Mandelbox set is a mathematical set defined by the iterations of points on a plane with a family of function \( T_\mu \), much like the famous Mandelbrot set after which its name is derived. The set can easily be generalized to any number of dimension and different values for the scale parameter \( \mu \) can lead to a wide range of different patterns.
While popular in the fractal art community, it has not yet been formally studied. In 1980, Benoit Mandelbrot generated the first image of the Mandelbrot set while working at IBM. Ron Eglash: The fractals at the heart of African designs. The Fractal Dimension of ZIP Codes. ZIP codes have been around for less than fifty years. In addition to allowing future historians to ascertain that the television show "Beverly Hills 90210" must have been created no earlier than 1963, ZIP codes have become part of our culture, organizing our locations and determining the flow of mail.
But ZIP codes are not created randomly. There is an order and a structure to this mail system. Hausdorff duminsion=fractal dimension? Fractal dimension of Mandelbulb, Mandelbox etc. It seems like a completion of the process to work out the fractal dimension for these fractals. It might not be that easy, it seems there are at least 5 variations of fractal dimension ( But I think the easiest procedure would be as follows:Set the max iterations to really high (so it doesn't affect the results)count the number of voxels with solid threshold at 1e-1, then again using e-2, e-3 etc.
Hausdorff dimension of the Mandelbulb. I assume everyone is discussing the boundary of the Mandelbulb here -- the boundary is fractal, whereas the interior is solid, with a dimension of exactly 3. Multifractal system. Multiplicative cascade. HABITONS-NOUS UN TROU NOIR ? Voir et comprendre en mathématiques. An Introduction to Fractals. A look into the fourth dimension. Ever since Albert Einstein developed the special theory of relativity in Zurich in 1905, by «fourth dimension» one usually means time.
Exploring 4D quantum Hall physics with a 2D topological charge pump. Infinite Cities VJ Pack. Ruins, Representation, and the Right to the City. Mandelbulb architecture. Borderless Worlds, Imagined Places: Bending Time and Space in the MCU. Fractalicious 6. Elemental Processing Unit. Prophecy (4K) Self Aware. Deep Time. Fractal Nature. Mandelbox- City at Dusk. Arbor — Jacob van Loon. Prophecy (4K) Chillout Tutorial: Fractal Formulas. Still Gallery — Julius Horsthuis. Crucifixion (Corpus Hypercubus) - Wikipedia. Fourth dimension in art - Wikipedia. Linda Henderson: Signs of the Fourth Dimension in 20th Century Art and Culture.
3 19 68 76 Apollinaire et la quatrieme dimension BOHN. Picard–Vessiot theory - Wikipedia. Dimension. The Fairyland of Geometry. Contrasting Concepts of Harmony in Architecture. PBS:The Elegant Universe 1 - Einstein's Dream. The Elegant Universe: Welcome to the 11th Dimension (Full HD Documentary) Images des mathématiques. Mandelbox370. Negative 1.5 Mandelbox - Mandelbox. Curvilinear perspective - Wikipedia. Marta Maas Fjetterstrom - Nazmiyal. Hvidtfeldts.net - generative art and systems, computational chemistry, machine learnings, physics... Algorithmic worlds. File:FWF Samuel Monnier détail.jpg - Wikipedia. Mathematics and art - Wikipedia.