

Vecteurs du plan et de l'espace (28 avril) - Vidéo Spécialités. Dans ce cours, la prof de maths Sophie propose d'étudier les vecteurs du plan et de l'espace.
Retrouvez le support de cours en PDF. Qu'est-ce qu'un vecteur ? Un vecteur est associé à une translation, un déplacement. C’est matérialisé par une flèche →u caractérisé par 3 informations : sa direction, son sens et ce que l’on appelle sa norme, c’est-à-dire sa longueur. Opérations possibles sur les vecteurs L’opposé d’un vecteur L’opposé du vecteur est le vecteur qui permet de faire le retour du point de vue de la translation. La somme de deux vecteurs On peut additionner 2 vecteurs →u et →v, en enchaînant les déplacements. La multiplication d’un vecteur par un réel On peut multiplier un vecteur par un nombre réel. Si je prends un nombre négatif, le vecteur obtenu n’aura pas le même sens, ni la même norme, mais la même direction. Vecteurs colinéaires. Vecteurs plan et espace. Chapitre 3 Manipuler des vecteurs des droites et des plans de l'espace. Page 66. Page 67. Page 68.
Page 69. Page 70. Page 71. Vidéo d'exercices d'une collègue pour ses élèves confinés. Exercices de révision pour le contrôle bilan n°1. Correction des exercices de révision pour le contrôle bilan n°1. Pistes page 466. Figure pour 127 p 71. Cube translations début. Cube quadrillé. Comb lin 3d. Cube N quadrillé (N peut varier) Caractérisation d'une droite D par un point et un vecteur directeur. K varie faisant décrire la droite à M. Géométrie dans l'espace - repère - vecteur colinéaire vecteur coplanaire cours en vidéo. Droites et plans de l'espace. 13 droites plans espace. 06 Vecteurs, droites et plans de l'espace. Fonction vectorielle de Leibniz - Homeomath. On appelle fonction vectorielle de Leibniz l'application qui à tout point M du plan (ou de l'espace ) associe le vecteur où α , β, γ sont trois réels fixés et A, B, C trois points fixés du plan (ou de l'espace).
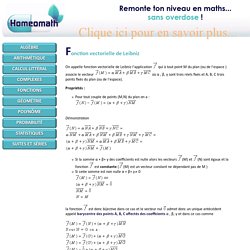
Propriétés : Pour tout couple de points (M,N) du plan on a : Démonstration Si la somme α + β+ γ des coefficients est nulle alors les vecteurs (M) et (N) sont égaux et la fonction est constante ((M) est un vecteur constant ne dépendant pas de M ) Si cette somme est non nulle α + β+ γ 0 la fonction est donc bijective dans ce cas et le vecteur nul admet donc un unique antécédent appelé barycentre des points A, B, C affectés des coefficients α , β, γ et dans ce cas comme Remarque : on peut généraliser la définition de cette fonction , quelque soit le nombre n de points ( n ≥ 2) : Pour , les propriétés restes analogues. Exemples de simplification vectorielle connaissant ou non un barycentre. Barycentre.