

Kovarianz (Stochastik) Sind und zwei reelle, integrierbare Zufallsvariablen, deren Produkt ebenfalls integrierbar ist, d. h., die Erwartungswerte existieren, dann heißt die Kovarianz von .
Quadratintegrierbar sind, also wenn gilt. Die Kovarianz ist positiv, wenn und einen monotonen Zusammenhang besitzen, d. h., hohe (niedrige) Werte von gehen mit hohen (niedrigen) Werten von einher.Die Kovarianz ist hingegen negativ, wenn und einen gegensinnigen monotonen Zusammenhang aufweisen, d. h., hohe Werte der einen Zufallsvariablen gehen mit niedrigen Werten der anderen Zufallsvariablen einher und umgekehrt.Ist das Ergebnis null, so besteht kein monotoner Zusammenhang zwischen und (Nichtmonotone Beziehungen sind aber möglich.). Erwartungswert. Er bestimmt die Lokalisation (Lage) der Verteilung der Zufallsvariablen und ist vergleichbar mit dem empirischen arithmetischen Mittel einer Häufigkeitsverteilung in der deskriptiven Statistik.
Er berechnet sich als nach Wahrscheinlichkeit gewichtetes Mittel der Werte, die die Zufallsvariable annimmt. Er muss selbst jedoch nicht einer dieser Werte sein. Insbesondere kann der Erwartungswert die Werte annehmen. Weil der Erwartungswert nur von der Wahrscheinlichkeitsverteilung abhängt, spricht man auch vom Erwartungswert einer Verteilung, ohne Bezug auf eine Zufallsvariable.
Motivation[Bearbeiten] Die Definition des Erwartungswerts steht in Analogie zum gewichteten Mittelwert von empirisch beobachteten Zahlen. Alternativ berechnet werden, indem man zunächst gleiche Werte zusammenfasst und nach ihrer relativen Häufigkeit gewichtet: Normalverteilung. Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ stetiger Wahrscheinlichkeitsverteilungen.
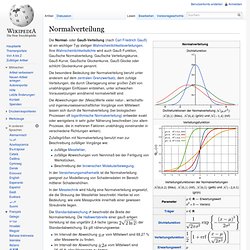
Ihre Wahrscheinlichkeitsdichte wird auch Gauß-Funktion, Gaußsche Normalverteilung, Gaußsche Verteilungskurve, Gauß-Kurve, Gaußsche Glockenkurve, Gauß-Glocke oder schlicht Glockenkurve genannt. Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, dem zufolge Verteilungen, die durch Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, unter schwachen Voraussetzungen annähernd normalverteilt sind. Die Abweichungen der (Mess)Werte vieler natur-, wirtschafts- und ingenieurswissenschaftlicher Vorgänge vom Mittelwert lassen sich durch die Normalverteilung (bei biologischen Prozessen oft logarithmische Normalverteilung) entweder exakt oder wenigstens in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).
Stochastischer Prozess. Definition[Bearbeiten] Sei ein Wahrscheinlichkeitsraum, .
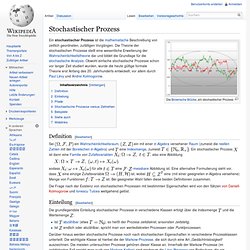
Ein stochastischer Prozess , also eine Abbildung sodass für alle. Lebesgue-Maß. Das Lebesgue-Maß Hintergrund[Bearbeiten] Das Lebesgue-Maß ist aus der Sicht der modernen Mathematik der natürliche Begriff für Flächeninhalt und Volumen.
Dieses Konzept ist das Endprodukt einer ganzen Reihe von Ideen, die versuchten, Begriffe wie Flächeninhalt und Volumen mathematisch exakt zu fassen. Erst mit dem Lebesgue-Maß kann dieser Prozess als abgeschlossen gelten. Das Lebesgue-Maß ordnet nicht nur einfachen geometrischen Objekten, sondern auch viel allgemeineren Mengen einschließlich aller offenen und abgeschlossenen Mengen einen Inhalt zu. Definition[Bearbeiten] Das Lebesgue-Borel-Maß auf der Borel-σ-Algebra mit der Eigenschaft d. h. das Maß, das Intervallen ihre Länge zuordnet (im Eindimensionalen), Rechtecken ihren Flächeninhalt zuordnet (im Zweidimensionalen), Quadern ihr Volumen zuordnet (im Dreidimensionalen), usw. für n-dimensionale Hyperquader.
Beliebiger Borel-Mengen eindeutig festgelegt. Dichtefunktion. In der Wahrscheinlichkeitstheorie ist die Wahrscheinlichkeitsdichtefunktion, oft kurz Dichtefunktion, Wahrscheinlichkeitsdichte oder nur Dichte (abgekürzt WDF oder pdf von engl. probability density function) genannt, ein Hilfsmittel zur Beschreibung einer stetigen Wahrscheinlichkeitsverteilung.
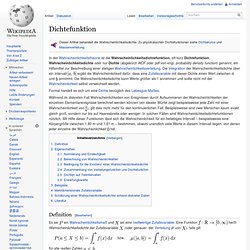
Die Integration der Wahrscheinlichkeitsdichte über ein Intervall ergibt die Wahrscheinlichkeit dafür, dass eine Zufallsvariable mit dieser Dichte einen Wert zwischen und annimmt. Die Wahrscheinlichkeitsdichte kann Werte größer als 1 annehmen und sollte nicht mit der Wahrscheinlichkeit selbst verwechselt werden. Formal handelt es sich um eine Dichte bezüglich des Lebesgue-Maßes. Während im diskreten Fall Wahrscheinlichkeiten von Ereignissen durch Aufsummieren der Wahrscheinlichkeiten der einzelnen Elementarereignisse berechnet werden können (ein idealer Würfel zeigt beispielsweise jede Zahl mit einer Wahrscheinlichkeit von ), gilt dies nicht mehr für den kontinuierlichen Fall.
Hat. Konvergenz (Stochastik) Wir werden die klassischen Konvergenzbegriffe immer im folgenden Modell formulieren: Gegeben sei eine Folge von Zufallsvariablen, die auf einem Wahrscheinlichkeitsraum definiert ist.
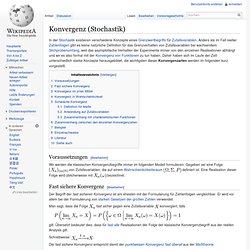
Eine Realisation dieser Folge wird üblicherweise mit bezeichnet. Der Begriff der fast sicheren Konvergenz ist am ehesten mit der Formulierung für Zahlenfolgen vergleichbar. Man sagt, dass die Folge fast sicher gegen eine Zufallsvariable konvergiert, falls. Definitheit. Definitheit von Bilinearformen und Sesquilinearformen[Bearbeiten] Es sei ein Vektorraum über den reellen (oder komplexen) Zahlen.
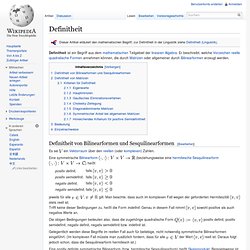
Eine symmetrische Bilinearform (beziehungsweise eine hermitesche Sesquilinearform ) heißt jeweils für alle , gilt. Stets reell ist. Sowohl positive als auch negative Werte an. Die obigen Bedingungen bedeuten also, dass die zugehörige quadratische Form positiv definit, positiv semidefinit, negativ definit, negativ semidefinit bzw. indefinit ist. Gelegentlich werden diese Begriffe im reellen Fall auch für beliebige, nicht notwendig symmetrische Bilinearformen eingeführt. Hauptachsentransformation. Ein zweischaliges Hyperboloid.
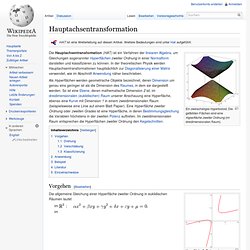
Die gefärbten Flächen sind eine Hyperfläche zweiter Ordnung (im dreidimensionalen Raum). Die Hauptachsentransformation (HAT) ist ein Verfahren der linearen Algebra, um Gleichungen sogenannter Hyperflächen zweiter Ordnung in einer Normalform darstellen und klassifizieren zu können. In der theoretischen Physik werden Hauptachsentransformationen hauptsächlich zur Diagonalisierung einer Matrix verwendet, wie im Abschnitt Anwendung näher beschrieben. Vorgehen[Bearbeiten] Hyperfläche 2. Die allgemeine Gleichung einer Hyperfläche zweiter Ordnung in euklidischen Räumen lautet im Theoretisch können Hauptachsentransformationen auch in unitären Räumen mit hermiteschen Matrizen über dem Körper der komplexen Zahlen durchgeführt werden, doch zur Vereinfachung und aus Gründen der Anschaulichkeit wird im Folgenden auf die analogen Vorgänge nicht eingegangen. Kovarianzmatrix. Ein Zufallsvektor, so ist die zugehörige Kovarianzmatrix gegeben durch Dabei bezeichnet die Kovarianz der reellen Zufallsvariablen und .
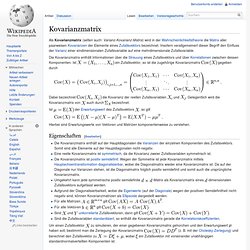
Auch durch bezeichnet.