

The Eye of the World Page 0,415 Read Online - Read The Eye of the World Page 0,415 Online for free. Them, and Lan bringing up the rear.

The hidden door swung hastily shut as soon as Mandarb stepped into the dirt alleyway. The snicksnick of latches locking, shutting them off, sounded unnaturally loud to Rand. The run, as Master Gill had called it, was very narrow indeed, and even darker than the stableyard, if that was possible. Tall, blank walls of brick or wood lined both sides, with only a narrow strip of black sky overhead. The big, woven baskets slung on the packhorse scraped the buildings on both sides. The partially filled lanterns sloshed with the motion of the horse, and clinked against each other with a tinny sound. When the run let out into a street, Loial chose his direction without a pause. As they hurried up the street Rand looked back toward the corner where The Queen's Blessing lay. Loial appeared to be following the most direct path to the Waygate, wherever it took them. The darkness began to lessen, fading toward a dark gray.
Comments ‹ Memory Athletes Association — WordPress. Stochastische Integration. Integralbegriffe nach Itō und Stratonovich[Bearbeiten] Seien.
Delta-Distribution. Definition[Bearbeiten] Der Testfunktionenraum für die Delta-Distribution ist der Raum der beliebig oft differenzierbaren Funktionen mit bzw. offen.
Somit entspricht entweder den reellen oder den komplexen Zahlen Die Delta-Distribution ordnet jeder beliebig oft differenzierbaren Funktion eine reelle bzw. komplexe Zahl zu, nämlich die Auswertung der Funktion an der Stelle 0. Liefert, schreibt man (mit der Notation der dualen Paarung) auch als beziehungsweise auch als Diese Schreibweise ist eigentlich nicht richtig und nur symbolisch zu verstehen, weil die Delta-Distribution eine irreguläre Distribution ist, das heißt sie lässt sich nicht durch eine lokal integrierbare Funktion in obiger Weise darstellen. , welche der obigen Definition genügt (für Beweis siehe unten „Irregularität“). Weißes Rauschen. Der Begriff zur Farbe weiß ist in übertragenen Sinn zu weißen Licht zu verstehen in welchen verschiedene optische Frequenzanteile sich zu einem weißen Farbeindruck überlagern.
Allerdings weist vom Menschen subjektiv empfundenes weißes Licht kein konstantes Leistungsdichtespektrum auf. Hörbeispiel von Weißen Gaußschen Rauschen. Korrelationskoeffizient. Der Korrelationskoeffizient (auch: Korrelationswert) oder die Produkt-Moment-Korrelation (von Bravais und Pearson, daher auch Pearson-Korrelation genannt) ist ein dimensionsloses Maß für den Grad des linearen Zusammenhangs zwischen zwei mindestens intervallskalierten Merkmalen.
Er kann Werte zwischen −1 und +1 annehmen. Bei einem Wert von +1 (bzw. −1) besteht ein vollständig positiver (bzw. negativer) linearer Zusammenhang zwischen den betrachteten Merkmalen. Wenn der Korrelationskoeffizient den Wert 0 aufweist, hängen die beiden Merkmale überhaupt nicht linear voneinander ab. Allerdings können diese ungeachtet dessen in nicht-linearer Weise voneinander abhängen. Lineare Abbildung. Achsenspiegelung als Beispiel einer linearen Abbildung ist die Summe der Vektoren und .
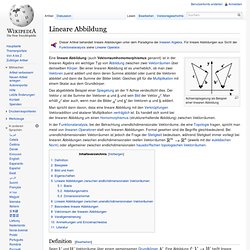
Man erhält aber auch, wenn man die Bilder der Vektoren addiert. In der Funktionalanalysis, bei der Betrachtung unendlichdimensionaler Vektorräume, die eine Topologie tragen, spricht man meist von linearen Operatoren statt von linearen Abbildungen. Wahrscheinlichkeitsfunktion. Ein Zufallsexperiment mit endlich oder abzählbar unendlich vielen möglichen Ausgängen lässt sich durch eine Wahrscheinlichkeitsfunktion (engl.: probability function oder probability mass function) beschreiben, welche für jeden Ausgang des Experiments dessen Auftretenswahrscheinlichkeit angibt.
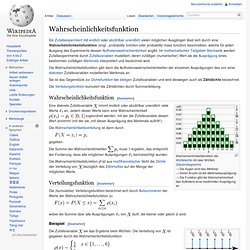
Im mathematischen Teilgebiet Stochastik werden Zufallsexperimente durch Zufallsvariablen modelliert, deren zufälliger (numerischer) Wert als die Ausprägung eines bestimmten zufälligen Merkmals interpretiert und bezeichnet wird. Die Wahrscheinlichkeitsfunktion gibt dann die Auftretenswahrscheinlichkeiten der einzelnen Ausprägungen des von einer diskreten Zufallsvariablen modellierten Merkmals an. Sie ist das Gegenstück zur Dichtefunktion bei stetigen Zufallsvariablen und wird deswegen auch als Zähldichte bezeichnet. Die Verteilungsfunktion kumuliert die Zähldichten durch Summenbildung. Wahrscheinlichkeitsfunktion[Bearbeiten] Eine diskrete Zufallsvariable. Zufallsvariable. Eine Zufallsvariable formalisiert damit ein Zufallsexperiment, dessen Zufallsergebnisse Zahlen generieren.
Auf Basis der Zufallsergebnisse sind damit insbesondere arithmetische Operationen und Größenvergleiche möglich. Beispiele für Zufallsvariablen sind die Augensumme von zwei geworfenen Würfeln (siehe unten) und die Gewinnhöhe in einem Glücksspiel. Verteilungsfunktion. Die Verteilungsfunktion ist eine der grundlegenden Begriffsbildungen der Wahrscheinlichkeitstheorie, wenngleich in neuerer Literatur der Fokus stärker auf Verteilungen selbst liegt.
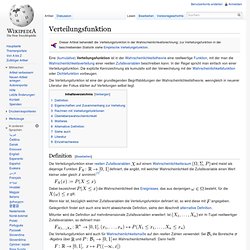
Definition[Bearbeiten] Die Verteilungsfunktion einer reellen Zufallsvariablen auf einem Wahrscheinlichkeitsraum wird meist als diejenige Funktion definiert, die angibt, mit welcher Wahrscheinlichkeit die Zufallsvariable einen Wert kleiner oder gleich annimmt:[1] Dabei bezeichnet besteht, für die gilt. Wenn klar ist, bezüglich welcher Zufallsvariablen die Verteilungsfunktion definiert ist, so wird diese mit angegeben. Gelegentlich findet sich auch eine leicht abweichende Definition, siehe den Abschnitt alternative Definition. Multivariate Verteilung. Die Wahrscheinlichkeitsverteilung einer mehrdimensionalen Zufallsvariablen nennt man multivariate Verteilung oder auch mehrdimensionale Verteilung.
Einführendes Beispiel[Bearbeiten] Wir betrachten zwei Zufallsexperimente. Das erste besteht aus einem zweimaligen Würfeln mit einem idealen Würfel. Dies ist äquivalent zu einem Urnenexperiment mit sechs unterscheidbaren Kugeln, wobei zweimal mit Zurücklegen gezogen wird. Gauß-Prozess. Ein Gaußprozess ist eine verallgemeinerte mehrdimensionale Gaußverteilung (nach Carl Friedrich Gauß) über unendlich viele Zufallsvariablen, von denen jede endliche Untermenge gaußverteilt ist. Während die mehrdimensionale Gaußverteilung eine Gaußverteilung von Vektoren darstellt, beschreibt ein Gaußprozess die Gaußverteilung eines Kontinuums von Zufallsvariablen und insbesondere eine Gaußverteilung von Funktionen. Angewendet werden Gaußprozesse häufig zur Interpolation, Extrapolation oder Glättung von diskreten Messpunkten. Die Besonderheit der Methode liegt darin, dass sie nahezu vollständig auf klassischer Wahrscheinlichkeitsrechnung beruht und sowohl die wahrscheinlichsten Werte vorhersagen kann, als auch die zugehörigen Unsicherheiten bzw.
Vertauensintervalle. Jede Eingangs- und Ausgangsgröße der Theorie setzt sich aus einem Wert und der Unsicherheit des Wertes zusammen, wobei stets die korrekte Fehlerfortpflanzung berücksichtigt wird. Definition[Bearbeiten]