

Problems on Trigonometric Identities with Solutions. To learn trigonometric identities in detail, click here Problem 1 : Prove : (1 - cos2θ) csc2θ = 1 Solution : Let A = (1 - cos2θ) csc2θ and B = 1.
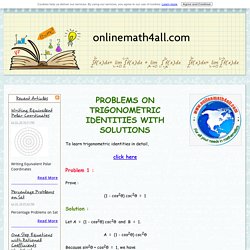
A = (1 - cos2θ) csc2θ Because sin2θ + cos2θ = 1, we have sin2θ = 1 - cos2θ Then, A = sin2θ ⋅ csc2θ A = sin2θ ⋅ (1/sin2θ) A = sin2θ /sin2θ A = B (Proved) Problem 2 : Let's Learn Right Triangle Trigonometry. In Figure 16.12.1, there is a circle centered at the origin with a radius whose length is r.

A radius has been drawn from the origin to a point on the circle in Quadrant I; the point is labeled (x,y). A right triangle has been created by dropping a line segment from the point (x,y) perpendicularly to x-axis. The angle of the triangle formed at the origin is labeled θ. The hypotenuse is labeled HYP. The side of the triangle that lies on the x-axis has been labeled ADJ which stands for "adjacent" as in it is the side other that the hypotenuse that is adjective to θ.
We can now redefine the trigonometric values of acute angles (angles whose measurements fall between 0∘ and 90∘, not including 0∘ nor 90∘). Exact Values of Trigonometric Functions - Questions With Answers. Exact Trig Values. This page is about the trigonometric functions of sine, cosine and tangent, what they are and how to find the exact values of many angles.

The calculators and other effects on this page require JavaScript but you appear to have switched JavaScript off (it is disabled) in this browser. Please go to the Preferences or Properties menu item for this browser and enable it and then Reload this page. What angles have an exact expression for their sines, cosines and tangents? You might know that cos(60°)=1/2 and sin(60°)=√3/2 as well as tan(45°)=1, but are 30, 45 and 60 the only angles up to 90° with a formula for their trig values? No! 1 A Table of Exact Trig values that are expressible as simple terms involving square-roots. 2 All the trig functions in one diagram Here is a really great Mathematica demonstration of how all the 6 trigonometric functions are related, in one interactive diagram. 2.1 Trig functions of Angles outside the range 0° to 90° Here is another visualization, by graphs: Phew! If. SAT Trigonometry: SOHCAHTOA and Radians.
Trigonometry and radians are new additions to the SAT Math section!
Do you love SOHCAHTOA and angle measurements? Do you hate trigonometry and radians and don't know what SOHCAHTOA or means? No matter how you feel about SAT trigonometry, there is no need to stress. In this guide, I'll let you know everything you need to know about trigonometry and radians for the SAT Math test and guide you through some practice problems. Trigonometric Formulas: Sine, Cosine, Tangent Although trigonometry makes up less than 5% of all math questions, you still want to get those questions right, and you won't be able to answer any trigonometry questions correctly without knowing the following formulas: Find the sine of an angle given the measures of the sides of the triangle.
In the figure above, the sine of the labeled angle would be Find the cosine of an angle given the measures of the sides of the triangle. In the figure above, the cosine of the labeled angle would be . Sine equals Opposite over Hypotenuse. Trigonometry Problem Solver. While we cover a very wide range of problems, we are currently unable to assist with this specific problem.
I spoke with my team and we will make note of this for future training. Is there a different problem you would like further assistance with? Mathway currently does not support this subject. We are more than happy to answer any math specific question you may have about this problem. Mathway currently does not support Ask an Expert Live in Chemistry. The 36 Trig Identities You Need to Know. If you’re taking a geometry or trigonometry class, one of the topics you’ll study are trigonometric identities.
There are numerous trig identities, some of which are key for you to know, and others that you’ll use rarely or never. This guide explains the trig identities you should have memorized as well as others you should be aware of. We also explain what trig identities are and how you can verify trig identities. In math, an "identity" is an equation that is always true, every single time. Trig identities are trigonometry equations that are always true, and they’re often used to solve trigonometry and geometry problems and understand various mathematical properties. The 25 Most Important Trig Identities Below are six categories of trig identities that you’ll be seeing often. Basic Identities These identities define the six trig functions. Pythagorean Identities Co-function Identities Each of the trig functions equals its co-function evaluated at the complementary angle.