

Entropy in thermodynamics and information theory. There are close parallels between the mathematical expressions for the thermodynamic entropy, usually denoted by S, of a physical system in the statistical thermodynamics established by Ludwig Boltzmann and J.

Willard Gibbs in the 1870s, and the information-theoretic entropy, usually expressed as H, of Claude Shannon and Ralph Hartley developed in the 1940s. Shannon, although not initially aware of this similarity, commented on it upon publicizing information theory in A Mathematical Theory of Communication. This article explores what links there are between the two concepts, and how far they can be regarded as connected. Equivalence of form of the defining expressions[edit] Boltzmann's grave in the Zentralfriedhof, Vienna, with bust and entropy formula. Algorithmic cooling. Algorithmic cooling is a phenomenon in quantum computation in which the processing of certain types of computation results in negative entropy and thus a cooling effect.
The phenomenon is a result of the connection between thermodynamics and information theory. In so far as information is encoded in physical systems it is subject to the laws of thermodynamics. Certain processes within computation require a change in entropy within the computing system. As data must be stored as some kind of ordered structure (like a localized charge in a capacitor) so the erasure of data by destroying this order must involve an increase in disorder, or entropy. This means that the erasure of data releases heat. Reversible computing or Adiabatic computing is a theoretical type of computing in which data is never erased, it just changes state or is marked to be ignored.
Simon's problem. In computational complexity theory and quantum computing, Simon's problem is a computational problem in the model of decision tree complexity or query complexity, conceived by Daniel Simon in 1994.[1] Simon exhibited a quantum algorithm, usually called Simon's algorithm, that solves the problem exponentially faster than any (deterministic or probabilistic) classical algorithm.
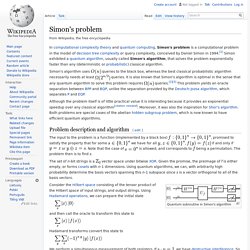
Simon's algorithm uses queries to the black box, whereas the best classical probabilistic algorithm necessarily needs at least queries. Quantum phase estimation algorithm. In quantum computing, the quantum phase estimation algorithm is a quantum algorithm that finds many applications as a subroutine in other algorithms.
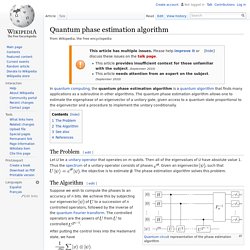
The quantum phase estimation algorithm allows one to estimate the eigenphase of an eigenvector of a unitary gate, given access to a quantum state proportional to the eigenvector and a procedure to implement the unitary conditionally. The Problem[edit] Let U be a unitary operator that operates on m qubits. Then all of the eigenvalues of U have absolute value 1. Deutsch–Jozsa algorithm. The Deutsch–Jozsa algorithm is a quantum algorithm, proposed by David Deutsch and Richard Jozsa in 1992[1] with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998.[2] Although of little practical use, it is one of the first examples of a quantum algorithm that is exponentially faster than any possible deterministic classical algorithm.
It is also a deterministic algorithm, meaning that it always produces an answer, and that answer is always correct. Problem statement[edit] In the Deutsch-Jozsa problem, we are given a black box quantum computer known as an oracle that implements the function . In layman's terms, it takes n-digit binary values as input and produces either a 0 or a 1 as output for each such value.
Is constant or balanced by using the oracle. Motivation[edit] Grover's algorithm. Grover's algorithm is a quantum algorithm that finds with high probability the unique input to a black box function that produces a particular output value, using just O(N1/2) evaluations of the function, where N is the size of the function's domain.
The analogous problem in classical computation cannot be solved in fewer than O(N) evaluations (because, in the worst case, the correct input might be the last one that is tried). At roughly the same time that Grover published his algorithm, Bennett, Bernstein, Brassard, and Vazirani published a proof that no quantum solution to the problem can evaluate the function fewer than O(N1/2) times, so Grover's algorithm is asymptotically optimal.[1] Unlike other quantum algorithms, which may provide exponential speedup over their classical counterparts, Grover's algorithm provides only a quadratic speedup. However, even quadratic speedup is considerable when N is large. Applications[edit] Setup[edit] Consider an unsorted database with N entries. And.
Toridion quantum compression crunches PNG image size by 50% For those of you who have not read about The Toridionite Project and who are interested in general discussion regarding the mathematics of quasi infinite data compression then check out the projects pages here.

For anyone else just read on. We are both proud and excited to announce that today in an experiment carried out in Spain. Toridion developers successfully reversibly compressed a randomized PNG image using the latest binaries of the Toridion “quantum data compression algorithm” Above, the rather mundane looking random PNG image used for todays experiment. Toridion took the 3152 bytes PNG compressed file and shrunk it by 50% without loss of any kind. The results were a conclusive success as Toridion quietly crunched the 3152 byte image by a breathtaking 50% in its first pass of encoding. Toridion uses no form of “RLE” or Run Length Encoding, where similar sequences of pixels are found and copied to reduce size.