

Laplacian of the indicator. In mathematics, the Laplacian of the indicator of the domain D is a generalisation of the derivative of the Dirac delta function to higher dimensions, and is non-zero only on the surface of D.
It can be viewed as the surface delta prime function. It is analogous to the second derivative of the Heaviside step function in one dimension. It can be obtained by letting the Laplace operator work on the indicator function of some domain D. The Maya way of forming a right angle. The great Mayan pyramid of Kukulcan "El Castillo" as seen from the Platform of the Eagles and Jaguars, Chichen Itza, Mexico.
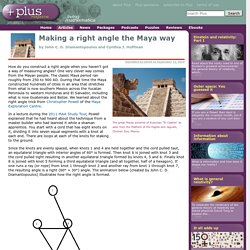
How do you construct a right angle when you haven't got a way of measuring angles? One very clever way comes from the Mayan people. The classic Maya period ran roughly from 250 to 900 AD. During that time the Maya constructed hundreds of cities in an area that stretches from what is now southern Mexico across the Yucatan Peninsula to western Honduras and El Salvador, including what is now Guatemala and Belize. We learned about the right angle trick from Christopher Powell of the Maya Exploration Centre. In a lecture during the 2011 MAA Study Tour, Powell explained that he had heard about the technique from a master builder who had learned it while a shaman apprentice. Since the knots are evenly spaced, when knots 1 and 4 are held together and the cord pulled taut, an equilateral triangle with interior angles of 60° is formed.
John C. About this article John C. Discrete event simulation. This contrasts with continuous simulation in which the simulation continuously tracks the system dynamics over time.
Instead of being event-based, this is called an activity-based simulation; time is broken up into small time slices and the system state is updated according to the set of activities happening in the time slice.[2] Because discrete-event simulations do not have to simulate every time slice, they can typically run much faster than the corresponding continuous simulation. A more recent method is the three-phased approach to discrete event simulation (Pidd, 1998). In this approach, the first phase is to jump to the next chronological event.
The second phase is to execute all events that unconditionally occur at that time (these are called B-events). The third phase is to execute all events that conditionally occur at that time (these are called C-events). Example[edit] Euler method. Illustration of the Euler method.

The unknown curve is in blue, and its polygonal approximation is in red. In mathematics and computational science, the Euler method is a SN-order[jargon] numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. List of Runge–Kutta methods. Dynamic errors of numerical methods of ODE discretization. The dynamical characteristic of the numerical method of ordinary differential equations (ODE) discretization – is the natural logarithm of its function of stability .
Dynamic characteristic is considered in three forms: – Complex dynamic characteristic; – Real dynamic characteristics; – Imaginary dynamic characteristics. General linear methods. General linear methods (GLMs) are a large class of numerical methods used to obtain numerical solutions to differential equations.
This large class of methods in numerical analysis encompass multistage Runge–Kutta methods that use intermediate collocation points, as well as linear multistep methods that save a finite time history of the solution. John C. Butcher originally coined this term for these methods, and has written a series of review papers[1] [2] [3] a book chapter[4] and a textbook[5] on the topic. His collaborator, Zdzislaw Jackiewicz also has an extensive textbook[6] on the topic. The original class of methods were originally proposed by Butcher(1965), Gear (1965) and Gragg and Stetter (1964). Some definitions[edit] Runge–Kutta methods. In numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods, which are used in temporal discretization for the approximation of solutions of ordinary differential equations.

These techniques were developed around 1900 by the German mathematicians C. Runge and M. W. Kutta. See the article on numerical methods for ordinary differential equations for more background and other methods. Monte Carlo method. Probabilistic problem-solving algorithm Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results.
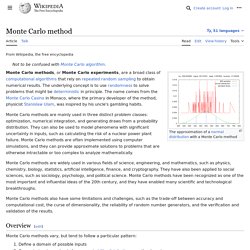
The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes:[1] optimization, numerical integration, and generating draws from a probability distribution. In principle, Monte Carlo methods can be used to solve any problem having a probabilistic interpretation. Linear multistep method. Linear multistep methods are used for the numerical solution of ordinary differential equations.

Conceptually, a numerical method starts from an initial point and then takes a short step forward in time to find the next solution point. The process continues with subsequent steps to map out the solution. Single-step methods (such as Euler's method) refer to only one previous point and its derivative to determine the current value.
Methods such as Runge–Kutta take some intermediate steps (for example, a half-step) to obtain a higher order method, but then discard all previous information before taking a second step. Multistep methods attempt to gain efficiency by keeping and using the information from previous steps rather than discarding it.