Linear optimization using R » Optimal Solution » finnstats. Linear optimization using R, in this tutorial we are going to discuss the linear optimization problems in R.
Optimization is everything nowadays. We all have finite resources and time and we want to make the maximum profit out of that. Companies want to makes maximum profits based on limited resources they have, yes optimization is the solution for that. Data scientists can provide optimal solutions based on given constraints to achieve maximum profit. Significance of Spearman’s Rank correlation Objective. The Beginner Programmer: Linear programming in R. Linear programming is a technique to solve optimization problems whose constraints and outcome are represented by linear relationships.

Simply put, linear programming allows to solve problems of the following kind: Maximize/minimize Under the constraint And the constraint This doesn’t seem much when you glance at it but in practice it is a powerful tool that can be used to make decisions in practical life scenarios. It is often the case that we need to make decisions based on constraints. Often the invisible and most harsh constraint is time, but generally speaking there are a lot of other constraints that we need to take into account.
I want to change my heating system. Field Guide to ILP Solvers in R for Conservation Prioritization. In this post I’ll compare alternative integer linear programming (ILP) solvers for conservation planning.

The goal is to develop a tool to solve the Marxan reserve design problem using ILP rather than simulated annealing. Unlike simulated annealing, ILP can find the true global optimum of an optimization problem or, if time constraints are an issue, it can return a solution that is within a specified distance form the optimum. This ability to evaluate the quality of a solution, makes IP an excellent candidate for conservation planning.
In a previous post, I demonstrated how to use the commercial optimization software Gurobi. Mixed Integer Programming in R with the ompr package. Choosing which method to use for “optimizing” functions – Blog: John C. Nash. A decision tree for function minimization What R calls “optimization” is more generally known as function minimization.
The tools in the stats package function optim() are all essentially function mimizers, as are those in the package optimrx found at optimrx tries to make it easier for users to call quite a few methods without having to learn many different sets of command syntax. It uses the same syntax as optim(), even down to parameter scaling, by changing the method=”name” argument. There are, however, a number of methods. Which is best for your purpose? Portfolio Optimization using R and Plotly. In this post we’ll focus on showcasing Plotly’s WebGL capabilities by charting financial portfolios using an R package called PortfolioAnalytics.
The package is a generic portfolo optimization framework developed by folks at the University of Washington and Brian Peterson (of the PerformanceAnalytics fame). You can see the vignette here. Quantitate: More on Quadratic Progamming in R. Journal of Statistical Software — Show. Vincent Zoonekynd's Blog. Fri, 01 Jun 2012: Optimization Many problems in statistics or machine learning are of the form "find the values of the parameters that minimize some measure of error".

But in some cases, constraints are also imposed on the parameters: for instance, that they should sum up to 1, or that at most 10 of them should be non-zero -- this adds a combinatorial layer to the problem, which makes it much harder to solve. In this note, I will give a guide to (some of) the optimization packages in R and explain (some of) the algorithms behind them. The solvers accessible from R have some limitations, such as the inability to deal with binary or integral constraints (in non-linear problems): we will see how to solve such problems. When you start to use optimization software, you struggle to coax the problem into the form expected by the software (you often have to reformulate it to make it linear or quadratic, and then write it in matrix form).
Introduction Local extrema Find x1,... The problem becomes. Optimization in R (Part I) This post is the first in a series on solving practical convex optimization problems with R.
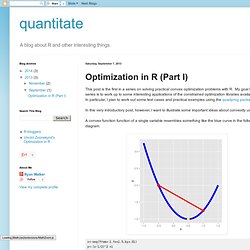
My goal for the series is to work up to some interesting applications of the constrained optimization libraries available in R. In particular, I plan to work out some test cases and practical examples using the quadprog package. In this very introductory post, however, I want to illustrate some important ideas about convexity using R. Notes on Optimization with R. Vincent Zoonekynd's Blog. Solving Quadratic Progams with R's quadprog package. In this post, we'll explore a special type of nonlinear constrained optimization problems called quadratic programs.
Quadratic programs appear in many practical applications, including portfolio optimization and in solving support vector machine (SVM) classification problems. There are several packages available to solve quadratic programs in R. Here, we'll work with the quadprog package. Before we dive into some examples with quadprog, we'll give a brief overview of the terminology and mechanics of quadratic programs. Quick Overview of Quadratic Programming In a quadratic programming problem, we consider a quadratic objective function: Q(x) = \frac{1}{2} x^T D x - d^T x + c. Here, x is a vector in \mathbb{R}^n, D is an n \times nsymmetric positive definite matrix, d is a constant vector in \mathbb{R}^n and c is a scalar constant. We also impose a system of linear constraints on the vector x \in \mathbb{R}^n. Example #1: Example #2: Let's inspect the optimal allocation: The Circus Tent Problem with R's Quadprog.
The MathWorks has an interesting demo on how the shape of a circus tent can be modeled as the solution of a quadratic program in MATLAB.