

The nth Term - Corbettmaths. Sequences - Finding A Rule. To find a missing number in a Sequence, first we must have a Rule Quick Definition of Sequence Read Sequences and Series for a more in-depth discussion, but put simply: A Sequence is a set of things (usually numbers) that are in order.
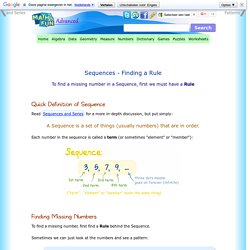
Each number in the sequence is called a term (or sometimes "element" or "member"): Finding Missing Numbers To find a missing number, first find a Rule behind the Sequence. Sometimes we can just look at the numbers and see a pattern: Example: 1, 4, 9, 16, ? Answer: they are Squares (12=1, 22=4, 32=9, 42=16, ...) Rule: xn = n2 Sequence: 1, 4, 9, 16, 25, 36, 49, ...
Did you see how we wrote that rule using "x" and "n" ? KS3 Bitesize Maths - Linear sequences : Revision, Page 3. Worksheet - Finding the nth term rule. To Be Continued. Algebra Generating a sequence given a rule 2. Algebra Generating a sequence given a rule 1. Sticky Triangles. Unit 7 Section 3 : Generating Number Sequences.
In this section you will find out how a formula can be used to give the terms of a sequence.
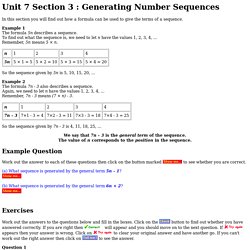
Example 1 The formula 5n describes a sequence. To find out what the sequence is, we need to let n have the values 1, 2, 3, 4, ... Remember, 5n means 5 × n. So the sequence given by 5n is 5, 10, 15, 20, ... Example 2 The formula 7n - 3 also describes a sequence. So the sequence given by 7n - 3 is 4, 11, 18, 25, ...
We say that 7n - 3 is the general term of the sequence. Example Question Work out the answer to each of these questions then click on the button marked to see whether you are correct. (a) What sequence is generated by the general term 5n - 1? (b) What sequence is generated by the general term 6n + 2? Exercises Work out the answers to the questions below and fill in the boxes. Button to find out whether you have answered correctly. Will appear and you should move on to the next question.
Appears then your answer is wrong. To clear your original answer and have another go. To see the answer. Chinese Dragon Game - Ordering and Sequencing Numbers. Algebra term to term rule. Number Patterns - 9-11 year olds. Number Sequences - Square, Cube and Fibonacci. Numbers can have interesting patterns.
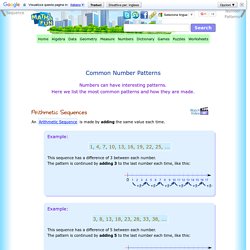
Here we list the most common patterns and how they are made. Arithmetic Sequences An Arithmetic Sequence is made by adding the same value each time. Example: This sequence has a difference of 3 between each number. This sequence has a difference of 5 between each number. The value added each time is called the "common difference" What is the common difference in this example? Answer: The common difference is 8 The common difference could also be negative: This common difference is −2 The pattern is continued by subtracting 2 each time, like this: Geometric Sequences A Geometric Sequence is made by multiplying by the same value each time. This sequence has a factor of 3 between each number. What we multiply by each time is called the "common ratio". In the previous example the common ratio was 3: We can start with any number: Example: Common Ratio of 3, But Starting at 2 This sequence also has a common ratio of 3, but it starts with 2.
Special Sequences. IXL - Complete a geometric number sequence (Year 6 maths practice)