

NP-Completeness. Algorithms. Hidden Markov Models - Online. Viterbi algorithm. The Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states – called the Viterbi path – that results in a sequence of observed events, especially in the context of Markov information sources and hidden Markov models.
The terms Viterbi path and Viterbi algorithm are also applied to related dynamic programming algorithms that discover the single most likely explanation for an observation. For example, in statistical parsing a dynamic programming algorithm can be used to discover the single most likely context-free derivation (parse) of a string, which is sometimes called the Viterbi parse. Example[edit] Consider a primitive clinic in a village. People in the village have a very nice property that they are either healthy or have a fever. Suppose a patient comes to the clinic each day and tells the doctor how she feels. The function viterbi takes the following arguments: obs is the sequence of observations, e.g.
Extensions[edit] to state . . If. The Viterbi Algorithm. Viterbi in java. Introduction to Algorithms. Dynamic programming. Dynamic Programming. This is the tenth post in an article series about MIT's lecture course "Introduction to Algorithms.
" In this post I will review lecture fifteen, which introduces the concept of Dynamic Programming and applies it to the Longest Common Subsequence problem. Dynamic programming is a design technique similar to divide and conquer. Divide-and-conquer algorithms partition the problem into independent subproblems, solve the subproblems recursively, and then combine their solutions to solve the original problem. Dynamic programming is applicable when the subproblems are not independent, that is, when subproblems share subsubproblems.
A dynamic-programming algorithm solves every subsubproblem just once and then saves its answer in a table, thereby avoiding the work of recomputing the answer every time the subsubproblem is encountered. Dynamic programming was systematized by Richard E. Dynamic programming is typically applied to optimization problems. 1. MIT's Introduction to Algorithms, Lecture 15 (visit www.catonmat.net for notes) Advanced Dynamic Programming. W'05 cs141: Cs141 Home. CS141 BB: CountingPathsByDP. Counting paths from a vertex S to a vertex T in a DAG (directed acyclic graph) How many distinct paths are there from S to T in this graph?

Each vertex is labeled with the number of paths from S to that vertex. Counting paths in a directed acyclic graph. Algorithm to find the number of distinct paths in a directed graph. Algo hw 16 solution. Book Article: Minimum Spanning Tree. Dijkstra's Shortest Path Calculator. By any measures, Edsgar Wybe Dijkstra was a remarkable man - one of the worlds undisputed leading computer scientist at the end of the 20th century, inventor of an operating system called ”THE”, that could have come straight from the script of one of the Airplane movies (“does it run on THE?

The what? The THE.”), long term chairman of his own fictional company that he described as the “most miserable business ever conceived” and originator of the meme-phrase “[insert pet hate here] considered harmful”. But one aspect of his work that has important historical significance is his development of algorithms. In 1959 Dijkstra published a short paper in Numerische Mathematik entitled ”A Note on Two Problems in Connexion with Graphs”. This is an interactive exploration of that algorithm intended to inspire interest and further reading, not a line by line exploration of the algorithm, though the code is available on github if you’d like to take that on.
Let’s start with that graph. Result : OK. Prim's algorithm. How to program Prim's algorithm for the Minimum Spanning Tree One of mascopt expected use is the quick implementation of algorithm and more partcularly algorithms on graphs.
This note is intended to help you in the realization of this goal by showing you how to manipulate the differents data structures involved. The followed approach is to show how one could program the Prim's algorithm that computes the Minimum Spanning Tree (MST for short) of a given graph. A formulation and a proof of this algorithm can be found in textbooks or even on the internet. Where we go. Algorithme de Prim. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir Prim. Prim's algorithm by Y. Jayarathina Madharasan. Algorithme de Kruskal. Un article de Wikipédia, l'encyclopédie libre.
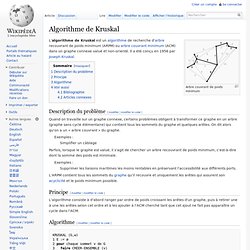
Arbre couvrant de poids minimum Description du problème[modifier | modifier le code] Quand on travaille sur un graphe connexe, certains problèmes obligent à transformer ce graphe en un arbre (graphe sans cycle élémentaire) qui contient tous les sommets du graphe et quelques arêtes. On dit alors qu'on a un « arbre couvrant » du graphe. Exemples : Simplifier un câblage Parfois, lorsque le graphe est valué, il s'agit de chercher un arbre recouvrant de poids minimum, c'est-à-dire dont la somme des poids est minimale. Supprimer les liaisons maritimes les moins rentables en préservant l'accessibilité aux différents ports.
L'ARPM contient tous les sommets du graphe qu'il recouvre et uniquement les arêtes qui assurent son acyclicité et le poids minimum possible. Principe[modifier | modifier le code] Algorithme[modifier | modifier le code] w est une fonction qui associe à chaque arête du graphe G une valeur qui est son poids. Thomas H. FibonacciHeap.java. Prim.java. Prim's Algorithm. The oldest and simplest MST algorithm was discovered by Boruvka in 1926.

The Boruvka's algorithm was rediscovered by Choquet in 1938; again by Florek, Lukaziewicz, Perkal, Stienhaus, and Zubrzycki in 1951; and again by Sollin in early 1960's. Minimum Spanning Tree Problem: Prim's Algorithm. Prim in java.