

TI-Nspire. Un article de Wikipédia, l'encyclopédie libre.
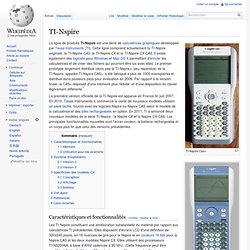
TI-Nspire Cas+ TI-Nspire avec clickpad. TI-Nspire CAS avec clickpad. TI-Nspire avec Touchpad. TI-Nspire CAS avec Touchpad. TI-Nspire CX CAS. TI-Nspire CX. La ligne de produits TI-Nspire est une série de calculatrices graphiques développée par Texas Instruments (TI). La première version officielle de la TI-Nspire est apparue en France fin juin 2007. Caractéristiques et fonctionnalités[modifier | modifier le code] Les TI-Nspire constituent une amélioration substantielle du matériel par rapport aux calculatrices TI précédentes.
Elles sont comparables à la TI-84 Plus du point de vue des caractéristiques et des fonctionnalités, et sont capables d'émuler une TI-84 au moyen d'un plugin et d'un clavier spécifique, inclus et interchangeable avec le clavier standard. Mémoire[modifier | modifier le code] Les deux calculateurs ont 16 Mo de mémoire flash NAND, 20 Mo de SDRAM, et 512 Ko de mémoire Flash NOR. Encyclopédie en ligne des suites de nombres entiers. Un article de Wikipédia, l'encyclopédie libre.
L'encyclopédie en ligne des suites de nombres entiers (originellement en anglais On-Line Encyclopedia of Integer Sequences, couramment abrégé sous le sigle OEIS) est un site web permettant d'effectuer gratuitement des recherches parmi une base de données de suites d'entiers présentant un intérêt mathématique ou parfois simplement ludique. Dans cette forme et cette présentation, c'est la plus grande du monde (en 2012). Elle est consultée des milliers de fois chaque jour.
L'OEIS est probablement la principale référence dans le domaine des suites d'entiers, pour les mathématiciens professionnels et amateurs, pour lesquels elle représente une ressource d'une très grande richesse. En particulier, une grande partie de son succès vient du fait qu'elle est accessible gratuitement. Description[modifier | modifier le code] Histoire[modifier | modifier le code] Il a publié deux sélections de sa collection sous forme de livre :
Ensemble de Julia. Un article de Wikipédia, l'encyclopédie libre.
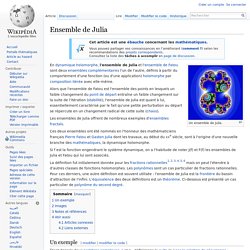
Un ensemble de Julia. Alors que l'ensemble de Fatou est l'ensemble des points en lesquels un faible changement du point de départ entraîne un faible changement sur la suite de l'itération (stabilité), l'ensemble de Julia est quant à lui, essentiellement caractérisé par le fait qu'une petite perturbation au départ se répercute en un changement radical de cette suite (chaos). Les ensembles de Julia offrent de nombreux exemples d'ensembles fractals.
Ces deux ensembles ont été nommés en l'honneur des mathématiciens français Pierre Fatou et Gaston Julia dont les travaux, au début du XXe siècle, sont à l'origine d'une nouvelle branche des mathématiques, la dynamique holomorphe. Si f est la fonction engendrant le système dynamique, on a l'habitude de noter J(f) et F(f) les ensembles de Julia et Fatou qui lui sont associés.
Un exemple[modifier | modifier le code] zn+1 = zn2 + c. Images[modifier | modifier le code] Voir aussi[modifier | modifier le code] Nombre complexe. Un article de Wikipédia, l'encyclopédie libre.
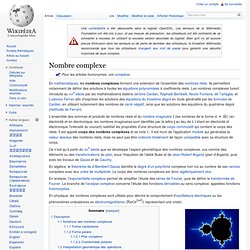
Pour les articles homonymes, voir complexe. L'ensemble des sommes et produits de nombres réels et du nombre imaginaire i (les nombres de la forme a + ib) (en électricité et en électronique, les nombres imaginaires sont identifiés par la lettre j au lieu de i, i étant en électricité et électronique l'intensité du courant) satisfait les propriétés d'une structure de corps commutatif qui contient le corps des réels.
Il est appelé corps des nombres complexes et se note ℂ. Il est muni de l'application module qui généralise la valeur absolue des nombres réels, mais ne peut pas être ordonné totalement de façon compatible avec sa structure de corps. En algèbre, le théorème de d'Alembert-Gauss identifie le degré d'un polynôme complexe non nul au nombre de ses racines comptées avec leur ordre de multiplicité. En analyse, l'exponentielle complexe permet de simplifier l'étude des séries de Fourier, puis de définir la transformée de Fourier.