

Rapid Prototyping Models. Background Rapid Prototyping or Solid Freeform Fabrication refers to a range of new technologies which construct physical three-dimensional objects by assembling thin layers of material under computer control.

Objects can be made which are extremely accurate, complex, and beautiful, and which no other technology can produce. For basic information on this rapidly evolving technology, I recommend this site or this site or search Google for new developments. Presently this is a somewhat expensive technology used mainly in high-end product design, and in research universities. But in the future, the cost will certainly come down and everyone will be able to create amazing physical objects with these machines. Mathematics As a sculptor I am necessarily interested in three-dimensional geometry. George W. Historical Models Art I am a sculptor and work with a wide range of materials, including RP designs.
Puzzles Algorithms. Bathsheba Sculpture. Éponge de Menger. Un article de Wikipédia, l'encyclopédie libre.
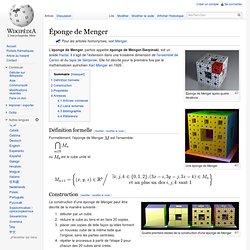
Pour les articles homonymes, voir Menger. Éponge de Menger après quatre itérations Une éponge de Menger L'éponge de Menger, parfois appelée éponge de Menger-Sierpinski, est un solide fractal. Il s'agit de l'extension dans une troisième dimension de l'ensemble de Cantor et du tapis de Sierpinski. Définition formelle[modifier | modifier le code] Formellement, l'éponge de Menger est l'ensemble: où est le cube unité et Construction[modifier | modifier le code] Quatre premiers stades de la construction d'une éponge de Menger La construction d'une éponge de Menger peut être décrite de la manière suivante : débuter par un cube,réduire le cube au tiers et en faire 20 copies,placer ces copies de telle façon qu'elles forment un nouveau cube de la même taille que l'original, sans les parties centrales,répéter le processus à partir de l'étape 2 pour chacun des 20 cubes ainsi créés.
Propriétés[modifier | modifier le code] Images des mathématiques. Un ballon de foot fractal. On a vu le Mandelbulb, le Mandelbox et voici maintenant une toute autre famille d’objets fractals. [1] Cette fois-ci, ce sont des polyèdres : les solides de Platon et des solides d’Archimède, mais aussi quelques formes plus exotiques.
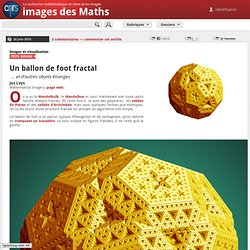
On va les munir d’une structure fractale en utilisant un algorithme très simple. Un ballon de foot a un patron typique d’hexagones et de pentagones, qu’on obtient en tronquant un icosaèdre. Le voici sculpté en figures fractales. Il ne reste qu’à le gonfler : Comment peut-on dessiner et sculpter ces objets ? Les polyèdres à la Wythoff Cette construction de Wythoff va nous aider dans ce qui suit. Un algorithme simple Ce que nous allons faire c’est prendre les trois plans qui passent par l’origine et par les côtés du triangle de base de la construction de Wythoff.
Aide-mémoire des polyèdres réguliers. On définit donc les trois plans et un point C sur la sphère à l’intérieur ou sur le bord du triangle défini par les trois plans. Associaèdre. Il y a cinq ans le Centre International de Rencontres Mathématiques de Luminy a envoyé ses vœux avec la carte ci-dessous.

L’illustration choisie par Robert Coquereaux, directeur du CIRM à cette époque là, était tout à fait adaptée pour l’an 5 du nouveau millénaire puisque ce polyèdre comporte plusieurs pentagones parmi ses faces. Mais intéressons-nous d’abord à des polygones et des polyèdres plus simples comme le triangle et le tétraèdre : Ils font partie d’une famille infinie de « polytopes » (les analogues des polygones et polyèdres en dimensions supérieures) appelés les simplexes standards.
Le n-simplexe standard {\mathcal{T}}^{n} peut être décrit de la manière suivante. Considérons les n+1 points de l’espace de dimension n+1 dont les coordonnées sont de la forme (0, \ldots , 0,1,0, \ldots , 0) ; plus précisément, on demande que chaque coordonnée soit nulle, sauf exactement une qui est égale à 1.
La structure de Weaire et Phelan. Lorsque les manchots empereurs, un œuf posé sur leurs pattes, bravent le froid en attendant que madame rapporte sa pêche, ils se serrent les uns contre les autres en un grand cercle mouvant ; ceux du bord s’insèrent pour se retrouver progressivement au centre, et ainsi de suite pour ne pas mourir de froid.

Cette position des manchots s’appelle la tortue. Sa forme circulaire est optimale, elle minimise la proportion de manchots sur le bord. Pour un nombre de manchots donné, le cercle minimise donc le nombre d’entre eux qui sont sur le pourtour de la zone occupée et ne peuvent se réchauffer au contact de leurs voisins. En termes mathématiques, si une courbe tracée dans le plan entoure une aire fixée , son périmètre est toujours supérieur à celui d’un cercle entourant un disque de même aire . La forme d’une bulle de savon s’adapte librement pour minimiser son énergie.