

Quaternion. Graphical representation of quaternion units product as 90°-rotation in 4D-space, ij = k, ji = −k, ij = −ji History[edit]
Per-Axis (Euler) Rotation Control While Avoiding Gimbal Lock? : Unity3D. Angle between two vectors. Using quaternion.AngleAxis. Quaternions: Not Satan. There are a lot of people working on cube puzzle games these days.

As the developer on Six Face, I am one of them. A game like this can cause you to come across challenges that you didn't know existed. One such challenge is understanding rotation in 3D space. Quaternions: Not Satan. Visualizing Quaternions with Unity. How do you model the position and orientation of an airplane?

Position is easy, just represent it with a point in 3D space. Rotating Objects Using Quaternions. Last year may go down in history as The Year of the Hardware Acceleration.
Much of the work rasterizing and texture-mapping polygons was off-loaded to dedicated hardware. How I learned to Stop Worrying and Love Quaternions. So you meet this cool API online somewhere.
It looks pretty fun, pretty powerful. Like just what you've been looking for. You dive in, you're having a good time, things are going great, when all of a sudden, BAM, it whips out a quaternion. Uh-oh You want to be cool and use it, but you don't really know what you're doing. Don't worry. It doesn't have to be like that though. Understanding Quaternions3D Game Engine Programming. Understanding Quaternions In this article I will attempt to explain the concept of Quaternions in an easy to understand way.
Avoiding Gimbal Lock. Mathematical reason behind gimbal lock in Euler angles. This article tries to explain gimbal lock from a mathematical perspective Mathematical singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability For example, the function f(x) = 1 / x on the real line has a singularity at x = 0, where it seems to “explode” to ±∞ and is not defined.
The function g(x) = |x| (see absolute value) also has a singularity at x = 0, since it is not differentiable there. Singularity is present in (2D) polar space, it occurs when r = 0, irrespective of the value of θ the resulting point would be the same, which is the origin. Euler angles are perfectly fine for orientation represention of objects, the problem of gimbal lock only occurs when trying to rotate using Euler angles, since linear interpolation from one orientation to another by interpolating the angles isn’t well-behaved due to the gimbal lock.
Versus. Gyroscope. Device for measuring or maintaining orientation and direction A gyroscope in operation.
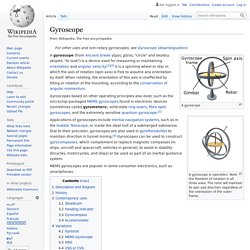
Note the freedom of rotation in all three axes. The rotor will maintain its spin axis direction regardless of the orientation of the outer frame. Gyroscopes based on other operating principles also exist, such as the microchip-packaged MEMS gyroscopes found in electronic devices (sometimes called gyrometers), solid-state ring lasers, fibre optic gyroscopes, and the extremely sensitive quantum gyroscope.[3] Applications of gyroscopes include inertial navigation systems, such as in the Hubble Telescope, or inside the steel hull of a submerged submarine. Zenith. Diagram showing the relationship between the zenith, the nadir, and different types of horizon.
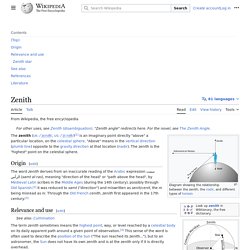
Note that the zenith is opposite the nadir. Zenith refers to an imaginary point directly "above" a particular location, on the imaginary celestial sphere. "Above" means in the vertical direction opposite to the apparent gravitational force at that location. The opposite direction, i.e. the direction in which gravity pulls, is toward the nadir. The zenith is the "highest" point on the celestial sphere (meaning it is the farthest up from the gravitational force). Origin[edit] The word "zenith" derives from the inaccurate reading of the Arabic expression سمت الرأس (samt ar-ra's), meaning "direction of the head" or "path above the head", by Medieval Latin scribes in the Middle Ages (during the 14th century), possibly through Old Spanish.[2] It was reduced to 'samt' ("direction") and miswritten as 'senit'/'cenit', as the "m" was misread as an "ni".
Relevance and Use[edit] See Also[edit] Euler (gimbal lock) Explained. Humane Rigging 03 - 3D Bouncy Ball 05 - Quaternion Rotation. Quaternions and 3D Rotations. The title of this tutorial is short and sweet.

The tutorial itself will not be. First, an introduction. Quaternions. Quaternions. This page is an introduction to Quaternions, the pages below this have more detail about their algebra and how to use them to represent 3D rotations. Introduction Quaternions were discovered on 16 October 1843 by William Rowan Hamilton. Euler Angles. We use the term "Euler Angle" for any representation of 3 dimensional rotations where we decompose the rotation into 3 separate angles. When we first start to think about 3D rotations this seems the natural way to proceed but our intuition can be deceptive and there are a lot of problems that arise when we use Euler angles to do calculations. If you are reading this page in order to write a 3D computer program I suggest you read enough of this page to convince yourself of the problems with Euler angles and to get an intuitive understanding of 3D rotations and then move on to quaternion or matrix algebra representations.
Understanding Euler Angles. 1. Introduction Attitude and Heading Sensors from CH Robotics can provide orientation information using both Euler Angles and Quaternions. Compared to quaternions, Euler Angles are simple and intuitive and they lend themselves well to simple analysis and control. Matrix. Description This snippet is my matrix class. I use this class when I can't get Unity's internal rotation and 3D math functions to do exactly what I want. It's pretty easy to use and the functions are discrete. Rotating 3D objects. A cube rotating about its z-axis.
Rotating things in three dimensions sounds complicated and it can be, but there are some simple rotations. For example, if we imagine rotating our cube around the z-axis (which points out of the screen), we are actually just rotating a square in two dimensions. There is a reason to learn trigonometry Rotating a point (x, 0) around the origin by θ. We can simplify things further, by just looking at a single node at position (x, 0). X' = x × cos(θ) Rotation About an Arbitrary Axis in 3 Dimensions.
Mesh from Vertices (Polygon from Spline) I am sharing Delaunay Triangulation Calculation maybe it can be helpful for others. Its useful for basic polygons. C# - Simple Voronoi/Delaunay Diagrams For Starters. Lloyd's algorithm. Delaunay - Voronoi Diagram library for Unity. Finding Points of Intersection. Finding Points of Intersection. Geometry - Finding a point along a line a certain distance away from another point! Equation of a line - point - slope form. (Coordinate Geometry)