

10 Coolest Mathematics Results. Technology Many people are put off by the obscure symbols and strict rules of math, giving up on a problem as soon as they see both numbers and letters involved.
But while math may be dense and difficult at times, the results it can prove are sometimes beautiful, mind-boggling, or just plain unexpected. Results like: The 4-Color Theorem was first discovered in 1852 by a man named Francis Guthrie, who at the time was trying to color in a map of all the counties of England (this was before the internet was invented, there wasn’t a lot to do). He discovered something interesting—he only needed a maximum of four colors to ensure that no counties that shared a border were colored the same. In 1976 (over a century later), this problem was finally solved by Kenneth Appel and Wolfgang Haken.
Brouwer’s Fixed Point Theorem This theorem comes from a branch of math known as Topology, and was discovered by Luitzen Brouwer. Remember Pythagoras’ theorem from school? Turing’s Universal Machine. Tesseract. Pigeons.jpg (JPEG Image, 640x380 pixels) The Value of Tardiness. Hypercube Projection. Hypercube. An n-dimensional hypercube is also called an n-cube or an n-dimensional cube.
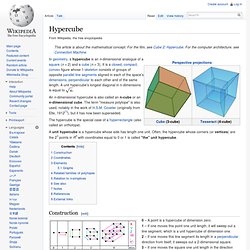
The term "measure polytope" is also used, notably in the work of H.S.M. Coxeter (originally from Elte, 1912[1]), but it has now been superseded. The hypercube is the special case of a hyperrectangle (also called an orthotope). A unit hypercube is a hypercube whose side has length one unit. Often, the hypercube whose corners (or vertices) are the 2n points in Rn with coordinates equal to 0 or 1 is called "the" unit hypercube. Construction[edit] A diagram showing how to create a tesseract from a point. An animation showing how to create a tesseract from a point. 0 – A point is a hypercube of dimension zero. 1 – If one moves this point one unit length, it will sweep out a line segment, which is a unit hypercube of dimension one. 2 – If one moves this line segment its length in a perpendicular direction from itself; it sweeps out a 2-dimensional square.
This can be generalized to any number of dimensions. . . Banach-Tarski Paradox. Did you know that it is possible to cut a solid ball into 5 pieces, and by re-assembling them, using rigid motions only, form TWO solid balls, EACH THE SAME SIZE AND SHAPE as the original?

This theorem is known as the Banach-Tarski paradox. So why can't you do this in real life, say, with a block of gold? If matter were infinitely divisible (which it is not) then it might be possible. But the pieces involved are so "jagged" and exotic that they do not have a well-defined notion of volume, or measure, associated to them. In fact, what the Banach-Tarski paradox shows is that no matter how you try to define "volume" so that it corresponds with our usual definition for nice sets, there will always be "bad" sets for which it is impossible to define a "volume"! Presentation Suggestions: Students will find this Fun Fact hard to believe.
The Math Behind the Fact: First of all, if we didn't restrict ourselves to rigid motions, this paradox would be more believable. Perfect numbers.