

Buy a Raspberry Pi 4 Model B – Raspberry Pi.
May trip. Quantum mechanics. Wavefunctions of the electron in a hydrogen atom at different energy levels.
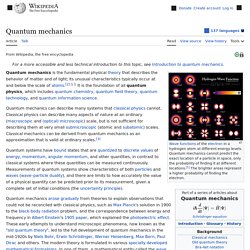
Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations.[1] The brighter areas represent a higher probability of finding the electron. Quantum mechanics (QM; also known as quantum physics, quantum theory, the wave mechanical model, or matrix mechanics), including quantum field theory, is a fundamental theory in physics which describes nature at the smallest scales of atoms and subatomic particles.[2]