

Ramanujan summation. Ramanujan summation is a technique invented by the mathematician Srinivasa Ramanujan for assigning a value to infinite divergent series.
Although the Ramanujan summation of a divergent series is not a sum in the traditional sense, it has properties that make it mathematically useful in the study of divergent infinite series, for which conventional summation is undefined. Summation[edit] Ramanujan summation essentially is a property of the partial sums, rather than a property of the entire sum, as that doesn't exist. If we take the Euler–Maclaurin summation formula together with the correction rule using Bernoulli numbers, we see that: Ramanujan[1] wrote it for the case p going to infinity: where C is a constant specific to the series and its analytic continuation and the limits on the integral were not specified by Ramanujan, but presumably they were as given above. Srinivasa Ramanujan. Srinivasa Ramanujan Iyengar FRS (pronunciation: i/sriː.ni.vaː.sə raː.maː.nʊ.dʒən/) (22 December 1887 – 26 April 1920) was an Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series, and continued fractions.
Ramanujan initially developed his own mathematical research in isolation; it was quickly recognized by Indian mathematicians. When his skills became apparent to the wider mathematical community, centred in Europe at the time, he began a famous partnership with the English mathematician G. H. Hardy. Early life[edit] Ramanujan's home on Sarangapani Street, Kumbakonam Ramanujan was born on 22 December 1887 in Erode, Madras Presidency (now Pallipalayam, Erode, Tamil Nadu), at the residence of his maternal grandparents in a Brahmin family.[5] His father, K. Since Ramanujan's father was at work most of the day, his mother took care of him as a child. Mr. For all. Ramanujan–Soldner constant. In mathematics, the Ramanujan–Soldner constant (also called the Soldner constant) is a mathematical constant defined as the unique positive zero of the logarithmic integral function.
It is named after Srinivasa Ramanujan and Johann Georg von Soldner. Its value is approximately μ ≈ 1.451369234883381050283968485892027449493… (sequence A070769 in OEIS) Since the logarithmic integral is defined by we have thus easing calculation for positive integers. Ramanujan–Petersson conjecture. In mathematics, the Ramanujan conjecture, due to Srinivasa Ramanujan (1916, p.176), states that Ramanujan's tau function given by the Fourier coefficients τ(n) of the cusp form Δ(z) of weight 12 satisfies when p is a prime number.
The generalized Ramanujan conjecture or Ramanujan–Petersson conjecture, introduced by Petersson (1930), is a generalization to other modular forms or automorphic forms. Ramanujan L-function[edit] The Riemann zeta function and the Dirichlet L-function satisfy the Euler product, and due to their completely multiplicative property Are there L-functions except for the Riemann zeta function and the Dirichlet L-functions satisfying the above relations? Ramanujan–Nagell equation. In mathematics, in the field of number theory, the Ramanujan–Nagell equation is a particular exponential Diophantine equation.
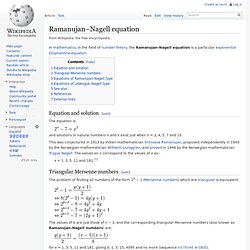
Equation and solution[edit] The equation is and solutions in natural numbers n and x exist just when n = 3, 4, 5, 7 and 15. This was conjectured in 1913 by Indian mathematician Srinivasa Ramanujan, proposed independently in 1943 by the Norwegian mathematician Wilhelm Ljunggren, and proved in 1948 by the Norwegian mathematician Trygve Nagell. The values on n correspond to the values of x as:- Ramanujan's sum. In number theory, a branch of mathematics, Ramanujan's sum, usually denoted cq(n), is a function of two positive integer variables q and n defined by the formula where (a, q) = 1 means that a only takes on values coprime to q.
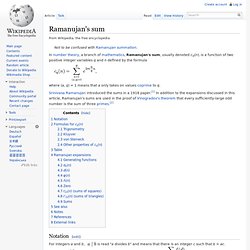
Srinivasa Ramanujan introduced the sums in a 1918 paper.[1] In addition to the expansions discussed in this article, Ramanujan's sums are used in the proof of Vinogradov's theorem that every sufficiently-large odd number is the sum of three primes.[2] Notation[edit] For integers a and b, is read "a divides b" and means that there is an integer c such that b = ac. Is read "a does not divide b". Means that d goes through all the positive divisors of m, e.g. Ramanujan's master theorem. Landau–Ramanujan constant. Heegner number. In number theory, a Heegner number is a square-free positive integer d such that the imaginary quadratic field Q(√−d) has class number 1.
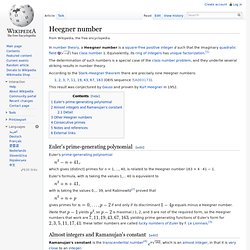
Equivalently, its ring of integers has unique factorization.[1] The determination of such numbers is a special case of the class number problem, and they underlie several striking results in number theory. According to the Stark–Heegner theorem there are precisely nine Heegner numbers: This result was conjectured by Gauss and proven by Kurt Heegner in 1952. Euler's prime-generating polynomial[edit] Euler's prime-generating polynomial which gives (distinct) primes for n = 1, ..., 40, is related to the Heegner number 163 = 4 · 41 − 1. 1729 (number) The two different ways are these: Of course, equating "smallest" with "most negative", as opposed to "closest to zero" gives rise to solutions like −91, −189, −1729, and further negative numbers.
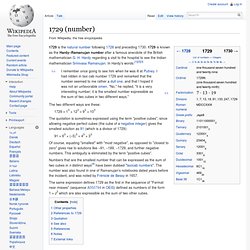
This ambiguity is eliminated by the term "positive cubes". Numbers that are the smallest number that can be expressed as the sum of two cubes in n distinct ways[4] have been dubbed "taxicab numbers". Ramanujan graph. , and the Petersen graph.
As Murty's survey paper notes, Ramanujan graphs "fuse diverse branches of pure mathematics, namely, number theory, representation theory, and algebraic geometry". As an example of this, a regular graph is Ramanujan if and only if its Ihara zeta function satisfies an analog of the Riemann hypothesis.[1] Definition[edit] Let be a connected -regular graph with vertices, and let. Ramanujan's congruences. Background[edit] In his 1919 paper (Ramanujan, 1919), he gave proof for the first two congruences using the following identities (using q-Pochhammer symbol notation): then stated that "It appears there are no equally simple properties for any moduli involving primes other than these".[1] After Ramanujan died in 1920, G.
H. Hardy, extracted proofs of all three congruences from an unpublished manuscript of Ramanujan on p(n) (Ramanujan, 1921). Extending results of A. Later Ken Ono conjectured that the elusive crank also satisfies exactly the same types of general congruences. A conceptual explanation for Ramanujan's observation was finally discovered in January 2011 [2] by considering the Hausdorff dimension of the following function in the l-adic topology: It is seen to have dimension 0 only in the cases where l = 5, 7 or 11 and since the partition function can be written as a linear combination of these functions[3] this can be considered a formalization and proof of Ramanujan's observation.
Ramanujan prime. In mathematics, a Ramanujan prime is a prime number that satisfies a result proven by Srinivasa Ramanujan relating to the prime-counting function. Origins and definition[edit]