

Photodissociation. This article is about molecular photodissociation.
The term "photodissociation" may also refer to nuclear photodissociation. Photodissociation, photolysis, or photodecomposition is a chemical reaction in which a chemical compound is broken down by photons. It is defined as the interaction of one or more photons with one target molecule. Photodissociation is not limited to visible light.
Pdf/cond-mat/0004293v2.pdf. Matter wave. The de Broglie relations redirect here.
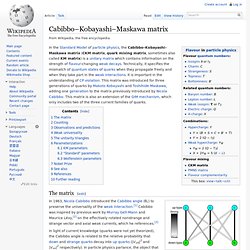
Physics.3.16. Cabibbo–Kobayashi–Maskawa matrix. The matrix[edit] A pictorial representation of the six quarks' decay modes, with mass increasing from left to right.
In 1963, Nicola Cabibbo introduced the Cabibbo angle (θc) to preserve the universality of the weak interaction.[1] Cabibbo was inspired by previous work by Murray Gell-Mann and Maurice Lévy,[2] on the effectively rotated nonstrange and strange vector and axial weak currents, which he references.[3] In light of current knowledge (quarks were not yet theorized), the Cabibbo angle is related to the relative probability that down and strange quarks decay into up quarks (|Vud|2 and |Vus|2 respectively). Pontryagin duality. In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle, or finite cyclic groups.
The Pontryagin duality theorem itself states that locally compact groups identify naturally with their bidual. The subject is named after Lev Semenovich Pontryagin who laid down the foundations for the theory of locally compact abelian groups and their duality during his early mathematical works in 1934. Pontryagin's treatment relied on the group being second-countable and either compact or discrete. This was improved to cover the general locally compact abelian groups by Egbert van Kampen in 1935 and André Weil in 1940.
Technicolor (physics) Technicolor theories are models of physics beyond the standard model that address electroweak gauge symmetry breaking, the mechanism through which W and Z bosons acquire masses.
Early technicolor theories were modelled on quantum chromodynamics (QCD), the "color" theory of the strong nuclear force, which inspired their name. In order to produce quark and lepton masses, technicolor has to be "extended" by additional gauge interactions. Particularly when modelled on QCD, extended technicolor is challenged by experimental constraints on flavor-changing neutral current and precision electroweak measurements. It is not known what is the extended technicolor dynamics. Much technicolor research focuses on exploring strongly interacting gauge theories other than QCD, in order to evade some of these challenges. Pontecorvo–Maki–Nakagawa–Sakata matrix. In particle physics, the Pontecorvo–Maki–Nakagawa–Sakata matrix (PMNS matrix), Maki–Nakagawa–Sakata matrix (MNS matrix), lepton mixing matrix, or neutrino mixing matrix, is a unitary matrix[note 1] which contains information on the mismatch of quantum states of leptons when they propagate freely and when they take part in the weak interactions.
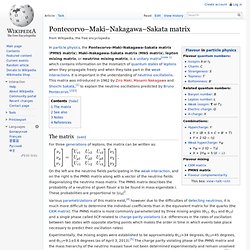
It is important in the understanding of neutrino oscillations. This matrix was introduced in 1962 by Ziro Maki, Masami Nakagawa and Shoichi Sakata,[1] to explain the neutrino oscillations predicted by Bruno Pontecorvo.[2][3] The matrix[edit] On the left are the neutrino fields participating in the weak interaction, and on the right is the PMNS matrix along with a vector of the neutrino fields diagonalizing the neutrino mass matrix. The PMNS matrix describes the probability of a neutrino of given flavor α to be found in mass eigenstate i. Based on less current data (28 June 2012) mixing angles are:[7] where NH indicates normal hierarchy and IH and.
Cosmology. Celestial Mechanics. General Relativity. Quantum Mechanics. String Theory. Casimir pressure. Casimir pressure is created by the Casimir force of virtual particles.
According to experiments, the Casimir force between two closely spaced neutral parallel plate conductors is directly proportional to their surface area. Phase space. Phase space of a dynamic system with focal instability, showing one phase space trajectory A plot of position and momentum variables as a function of time is sometimes called a phase plot or a phase diagram.
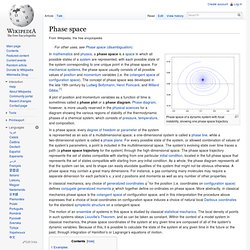
Phase diagram, however, is more usually reserved in the physical sciences for a diagram showing the various regions of stability of the thermodynamic phases of a chemical system, which consists of pressure, temperature, and composition. In classical mechanics, any choice of generalized coordinates q i for the position (i.e. coordinates on configuration space) defines conjugate generalized momenta pi which together define co-ordinates on phase space.
Homogeneity (physics) The definition of homogeneous strongly depends on the context used.
For example, a composite material is made up of different individual materials, known as "constituents" of the material, but may be defined as a homogeneous material when assigned a function. For example, asphalt paves our roads, but is a composite material consisting of asphalt binder and mineral aggregate, and then laid down in layers and compacted. In another context, a material is not homogeneous in so far as it composed of atoms and molecules. However, at the normal level of our everyday world, a pane of glass, or a sheet of metal is described as glass, or stainless steel. In other words, these are each described as a homogeneous material. Lamb–Oseen vortex. In fluid dynamics, the Lamb–Oseen vortex models a line vortex that decays due to viscosity.
This vortex is named after Horace Lamb and Carl Wilhelm Oseen.[1] Lorentz group. Digital physics. Digital physics is grounded in one or more of the following hypotheses; listed in order of decreasing strength. The universe, or reality: Non-orientable wormhole. In topology, this sort of connection is referred to as an Alice handle. Theory[edit] "Normal" wormhole connection[edit] Matt Visser has described a way of visualising wormhole geometry: take a "normal" region of space"surgically remove" spherical volumes from two regions ("spacetime surgery")associate the two spherical bleeding edges, so that a line attempting to enter one "missing" spherical volume encounters one bounding surface and then continues outward from the other. Scharnhorst effect. The Scharnhorst effect is a hypothetical phenomenon in which light signals travel faster than c between two closely spaced conducting plates.
It was predicted by Klaus Scharnhorst of the Humboldt University of Berlin, Germany, and Gabriel Barton of the University of Sussex in Brighton, England. They showed using quantum electrodynamics that the effective refractive index, at low frequencies, in the space between the plates was less than 1 (which by itself does not imply superluminal signaling). They were not able to show that the wavefront velocity exceeds c (which would imply superluminal signaling) but argued that it is plausible.[1] Explanation[edit] Owing to Heisenberg's uncertainty principle, an empty space which appears to be a true vacuum is actually filled with virtual subatomic particles.
The effect, however, is predicted to be minuscule. Fredkin finite nature hypothesis. In digital physics, the Fredkin Finite Nature Hypothesis states that ultimately all quantities of physics, including space and time, are discrete and finite. All measurable physical quantities arise from some Planck scale substrate for multiverse information processing. Also, the amount of information in any small volume of spacetime will be finite and equal to a small number of possibilities.[1] Conceptions[edit] Stephen Wolfram in A New Kind of Science, Chapter 9, considered the possibility that energy and spacetime might be secondary derivations from an informational substrate underlying the Planck scale.