

Euclid's lemma. This property is the key[1] in the proof of the fundamental theorem of arithmetic.
It is used to define prime elements, a generalization of prime numbers to arbitrary commutative rings. The lemma is not true for composite numbers. For example, 4 does not divide 6 and 4 does not divide 10, yet 4 does divide their product, 60. Formulations[edit] Let p be a prime number, and assume p divides the product of two integers a and b. Equivalent statements are If p∤a and p∤b, then p∤ab. A generalization is also called Euclid's lemma: If n|ab, and n is relatively prime to a, then n|b. N|a orn is relatively prime to a. History[edit] The lemma first appears as proposition 30 in Book VII of Euclid's Elements. Proof via Bézout's identity[edit] The usual proof involves another lemma called Bézout's identity.
Let a and n be relatively prime, and assume that n | ab. Multiply both sides by b: See also[edit] Euclidean algorithm Notes[edit] References[edit] Gauss, Carl Friedrich; Clarke, Arthur A. Prime gap. A prime gap is the difference between two successive prime numbers.
The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-th and the n-th prime numbers, i.e. We have g1 = 1, g2 = g3 = 2, and g4 = 4. The sequence (gn) of prime gaps has been extensively studied, however many questions and conjectures remain unanswered. The first 30 prime gaps are: By the definition of gn the following sum can be stated as Simple observations[edit] The first, smallest, and only odd prime gap is 1 between the only even prime number, 2, and the first odd prime, 3. Is a sequence of Q − 2 consecutive composite integers, so here there is a prime gap of at least length Q − 1. In reality, prime gaps of P numbers can occur at numbers much smaller than P#. Primorial. Pn# as a function of n, plotted logarithmically. n# as a function of n (red dots), compared to n!.
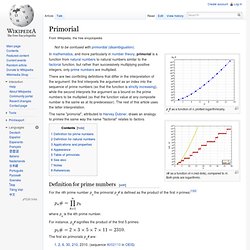
Both plots are logarithmic. In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, only prime numbers are multiplied. There are two conflicting definitions that differ in the interpretation of the argument: the first interprets the argument as an index into the sequence of prime numbers (so that the function is strictly increasing), while the second interprets the argument as a bound on the prime numbers to be multiplied (so that the function value at any composite number is the same as at its predecessor). The rest of this article uses the latter interpretation. The name "primorial", attributed to Harvey Dubner, draws an analogy to primes the same way the name "factorial" relates to factors. Definition for prime numbers[edit] where Since. Prime number.
A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself.
A natural number greater than 1 that is not a prime number is called a composite number. For example, 5 is prime because 1 and 5 are its only positive integer factors, whereas 6 is composite because it has the divisors 2 and 3 in addition to 1 and 6. The fundamental theorem of arithmetic establishes the central role of primes in number theory: any integer greater than 1 can be expressed as a product of primes that is unique up to ordering. The uniqueness in this theorem requires excluding 1 as a prime because one can include arbitrarily many instances of 1 in any factorization, e.g., 3, 1 × 3, 1 × 1 × 3, etc. are all valid factorizations of 3. The property of being prime (or not) is called primality. . Definition and examples.