

Embree–Trefethen constant. In number theory, the Embree–Trefethen constant is a threshold value labelled β*.[1] For a fixed positive number β, consider the recurrence relation where the sign in the sum is chosen at random for each n independently with equal probabilities for "+" and "−".
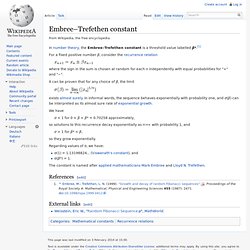
It can be proven that for any choice of β, the limit exists almost surely. In informal words, the sequence behaves exponentially with probability one, and σ(β) can be interpreted as its almost sure rate of exponential growth. We have σ < 1 for 0 < β < β* = 0.70258 approximately, so solutions to this recurrence decay exponentially as n→∞ with probability 1, and σ > 1 for β* < β, so they grow exponentially. Mathematical constants by continued fraction representation. This is a list of mathematical constants sorted by their representations as continued fractions.
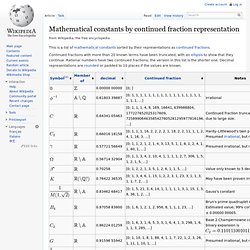
Continued fractions with more than 20 known terms have been truncated, with an ellipsis to show that they continue. Rational numbers have two continued fractions; the version in this list is the shorter one. Decimal representations are rounded or padded to 10 places if the values are known. Jump up ^ Although some of the symbols in the leftmost column are displayed in black due to math markup peculiarities, all are clickable and link to the respective constant's page.
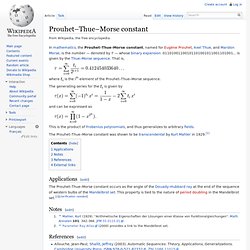
Prouhet–Thue–Morse constant. In mathematics, the Prouhet–Thue–Morse constant, named for Eugène Prouhet, Axel Thue, and Marston Morse, is the number — denoted by — whose binary expansion .01101001100101101001011001101001... is given by the Thue–Morse sequence.
Reciprocal Fibonacci constant. The ratio of successive terms in this sum tends to the reciprocal of the golden ratio.
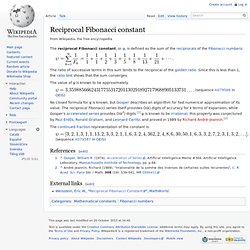
Since this is less than 1, the ratio test shows that the sum converges. The value of ψ is known to be approximately (sequence A079586 in OEIS) No closed formula for ψ is known, but Gosper describes an algorithm for fast numerical approximation of its value. The reciprocal Fibonacci series itself provides O(k) digits of accuracy for k terms of expansion, while Gosper's accelerated series provides O(k2) digits.[1] ψ is known to be irrational; this property was conjectured by Paul Erdős, Ronald Graham, and Leonard Carlitz, and proved in 1989 by Richard André-Jeannin.[2]
Ring of periods. Maxim Kontsevich and Don Zagier (2001) gave a survey of periods and introduced some conjectures about them.
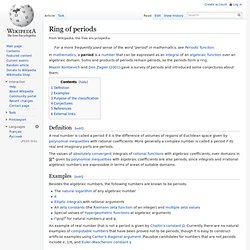
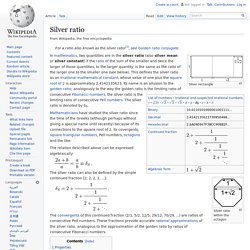
Definition[edit] The values of absolutely convergent integrals of rational functions with algebraic coefficients, over domains in Examples[edit] Besides the algebraic numbers, the following numbers are known to be periods: The natural logarithm of any algebraic numberπElliptic integrals with rational argumentsAll zeta constants (the Riemann zeta function of an integer) and multiple zeta valuesSpecial values of hypergeometric functions at algebraic argumentsΓ(p/q)q for natural numbers p and q. Silver ratio. Silver ratio within the octagon In mathematics, two quantities are in the silver ratio (also silver mean or silver constant) if the ratio of the sum of the smaller and twice the larger of those quantities, to the larger quantity, is the same as the ratio of the larger one to the smaller one (see below).
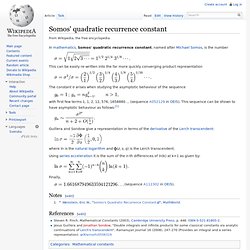
Somos' quadratic recurrence constant. In mathematics, Somos' quadratic recurrence constant, named after Michael Somos, is the number This can be easily re-written into the far more quickly converging product representation The constant σ arises when studying the asymptotic behaviour of the sequence with first few terms 1, 1, 2, 12, 576, 1658880 ...
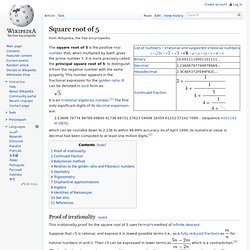
(sequence A052129 in OEIS). This sequence can be shown to have asymptotic behaviour as follows:[1] Square root of 5. It is an irrational algebraic number.[1] The first sixty significant digits of its decimal expansion are: 2.23606 79774 99789 69640 91736 68731 27623 54406 18359 61152 57242 7089...
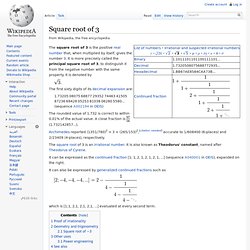
(sequence A002163 in OEIS). which can be rounded down to 2.236 to within 99.99% accuracy. As of April 1994, its numerical value in decimal had been computed to at least one million digits.[2] Square root of 3. The first sixty digits of its decimal expansion are: 1.73205 08075 68877 29352 74463 41505 87236 69428 05253 81038 06280 5580...
Square root of 2. "Pythagoras's constant" redirects here; not to be confused with Pythagoras number The square root of 2, often known as root 2, radical 2, or Pythagoras' constant, and written as Geometrically the square root of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem.
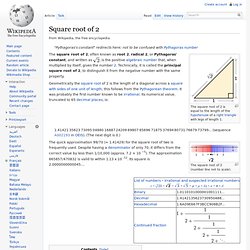
It was probably the first number known to be irrational. Its numerical value, truncated to 65 decimal places, is: 1.41421356237309504880168872420969807856967187537694807317667973799... Stieltjes constants. In mathematics, the Stieltjes constants are the numbers that occur in the Laurent series expansion of the Riemann zeta function: The zero'th constant is known as the Euler–Mascheroni constant.
Representations[edit] (In the case n = 0, the first summand requires evaluation of 00, which is taken to be 1.) Cauchy's differentiation formula leads to the integral representation Several representations in terms of integrals and infinite series are given in the papers of Coffey. Numerical values[edit] The first few values are: For large n, the Stieltjes constants grow rapidly in absolute value, and change signs in a complex pattern. Numerical values of the Stieltjes constants up to n = 100000, accurate to over 10000 digits each, have been computed by Johansson.
Asymptotic growth[edit] Twelfth root of two. The twelfth root of two or is an algebraic irrational number. It is most important in music theory, where it represents the frequency ratio of a semitone in Twelve-tone equal temperament. Numerical value[edit] Its value is 1.05946309435929..., which is slightly more than 18⁄17 ≈ 1.0588. Better approximations are 196⁄185 ≈ 1.059459 or 18904⁄17843 ≈ 1.0594630948.
Universal parabolic constant. The universal parabolic constant is a mathematical constant. The value of P is Derivation[edit] Take.