

Morphism. In category theory, morphism is a broadly similar idea, but somewhat more abstract: the mathematical objects involved need not be sets, and the relationship between them may be something more general than a map.
Complete metric space. In mathematical analysis, a metric space M is called complete (or a Cauchy space) if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M. Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary).
For instance, the set of rational numbers is not complete, because e.g. √2 is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it. (See the examples below.) It is always possible to "fill all the holes", leading to the completion of a given space, as explained below. Examples[edit] Group (mathematics) Groups share a fundamental kinship with the notion of symmetry.
For example, a symmetry group encodes symmetry features of a geometrical object: the group consists of the set of transformations that leave the object unchanged and the operation of combining two such transformations by performing one after the other. Lie groups are the symmetry groups used in the Standard Model of particle physics; Point groups are used to help understand symmetry phenomena in molecular chemistry; and Poincaré groups can express the physical symmetry underlying special relativity.
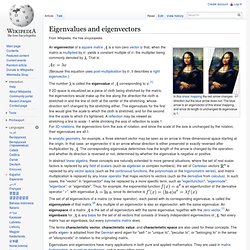
Eigenvalues and eigenvectors. In this shear mapping the red arrow changes direction but the blue arrow does not.
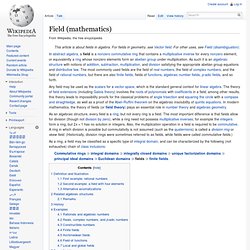
Field theory (mathematics) Commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ finite fields.
Intuitively, a field is a set F that is a commutative group with respect to two compatible operations, addition and multiplication, with "compatible" being formalized by distributivity, and the caveat that the additive identity (0) has no multiplicative inverse (one cannot divide by 0). Closure of F under addition and multiplication For all a, b in F, both a + b and a · b are in F (or more formally, + and · are binary operations on F). Free algebra. In mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring (which may be regarded as a free commutative algebra).
Definition[edit] and the product of two arbitrary elements is thus uniquely determined (because the multiplication in an R-algebra must be R-bilinear). This R-algebra is denoted R⟨X1,...,Xn⟩. This construction can easily be generalized to an arbitrary set X of indeterminates. In short, for an arbitrary set with the R-bilinear multiplication that is concatenation on words, where X* denotes the free monoid on X (i.e. words on the letters Xi), Prime ideal. Invariant basis number. Definition[edit] Equivalently, this means there do not exist distinct positive integers m and n such that Rm is isomorphic to Rn.
Rephrasing the definition of invariant basis number in terms of matrices, it says that, whenever A is an m by n matrix over R and B is an n by m matrix over R such that AB=1 and BA=1, then m=n. This form reveals that the definition is left-right symmetric, so it makes no difference whether we define IBN in terms of left or right modules; the two definitions are equivalent. Dynkin diagram. The term "Dynkin diagram" can be ambiguous.
In some cases, Dynkin diagrams are assumed to be directed, in which case they correspond to root systems and semi-simple Lie algebras, while in other cases they are assumed to be undirected, in which case they correspond to Weyl groups; the and directed diagrams yield the same undirected diagram, correspondingly named In this article, "Dynkin diagram" means directed Dynkin diagram, and undirected Dynkin diagrams will be explicitly so named. Classification of semisimple Lie algebras[edit] The fundamental interest in Dynkin diagrams is that they classify semisimple Lie algebras over algebraically closed fields. Lie group. Orthogonality. The line segments AB and CD are orthogonal to each other.
The concept of orthogonality has been broadly generalized in mathematics, science, and engineering, especially since the beginning of the 16th century. Much of the generalizing has taken place in the areas of mathematical functions, calculus and linear algebra. Etymology[edit] The word comes from the Greek ὀρθός (orthos), meaning "upright", and γωνία (gonia), meaning "angle". The ancient Greek ὀρθογώνιον orthogōnion (< ὀρθός orthos 'upright'[1] + γωνία gōnia 'angle'[2]) and classical Latin orthogonium originally denoted a rectangle.[3] Later, they came to mean a right triangle. Mathematics[edit] Definitions[edit] Orbifold notation. In geometry, orbifold notation (or orbifold signature) is a system, invented by William Thurston and popularized by the mathematician John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature.
Homeomorphism group. Group isomorphism. Definition and notation[edit] Given two groups (, ∗) and (, ), a group isomorphism from (, ∗) to (, ) is a bijective group homomorphism from to .
Isomorphism. The group of fifth roots of unity under multiplication is isomorphic to the group of rotations of the pentagon under composition. In mathematics, an isomorphism, from the Greek: ἴσος isos "equal", and μορφή morphe "shape", is a homomorphism (or more generally a morphism) that admits an inverse. [note 1] Two mathematical objects are isomorphic if an isomorphism exists between them.
An automorphism is an isomorphism whose source and target coincide. The interest of isomorphisms lies in the fact that two isomorphic objects cannot be distinguished by using only the properties used to define morphisms; thus isomorphic objects may be considered the same as long as one considers only these properties and their consequences. In topology, where the morphisms are continuous functions, isomorphisms are also called homeomorphisms or bicontinuous functions. Isomorphisms are formalized using category theory. Examples[edit] Logarithm and exponential[edit] Let.
Heap (mathematics) Which satisfies the para-associative law. Klein four-group. The Klein four-group is the smallest non-cyclic group. It is given by the group presentation All non-identity elements of the Klein group have order 2. It is abelian, and isomorphic to the dihedral group of order (cardinality) 4. It is also isomorphic to the direct sum Z2 ⊕ Z2, so that it can be represented as the bit strings {00, 01, 10, 11} under bitwise XOR.