

Brilliant Math & Science Wiki. Under classical principles, all participants are assumed to have the common knowledge of perfect rationality, meaning that every player is aware that other players are perfectly rational (and that they are aware that other players are aware that other players are rational, etc.).
However, this is not usually the case in practical settings, as equilibrium rarely occurs in actual play. In fact, the perfectly rational agent is often at a disadvantage, since they overestimate the depth of other players. For example, in the '2/3 of the average' game described in the previous section, classical principles would suggest that the perfectly rational agent would select the number 0. However, the winning number is usually much higher in practice. For example, 21.6 was the winning guess in a competition with over 19,000 participants [1], which is slightly below the number a level-2 thinker would select. Brilliant Math & Science Wiki. If where and are constants such that and which of the following could be the graph of ?
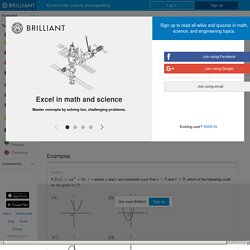
Solution: Tip: The parabola opens down if Tip: The parabola has a intercept at Because the parabola opens downward, and we can eliminate choices (A) and (B) where this is not the case. If we set , then . Hence, is the y-intercept. We are told that . In choice (D), and in choice (E), Therefore we can eliminate them. The graphs of and intersect at point where is a constant. Incorrect Choices: (A), (B), (C), and (D) Solution 2 eliminates these choices by plugging and checking. Divisibliity Rules (2,3,5,7,11,13,17,19,...) A positive integer is divisible by if the last digit of is 2, 4, 6, 8, or 0; if the sum of digits of is a multiple of 3; if the last 2 digits of are a multiple of 4; if the last digit of is either 0 or 5; if is divisible by both 2 and 3; if subtracting twice the last digit of from the remaining digits gives a multiple of 7 (e.g. 658 is divisible by 7 because 65 - 2 x 8 = 49, which is a multiple of 7); if the last 3 digits of are a multiple of 8; if the sum of digits of is a multiple of 9; if the last digit of is 0; if the difference of the alternating sum of digits of is a multiple of 11 (e.g. 2343 is divisible by 11 because 2 - 3 + 4 - 3 = 0, which is a multiple of 11); if is divisible by both 3 and 4.
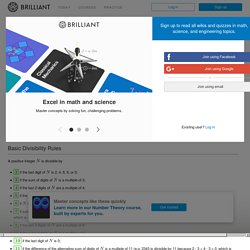
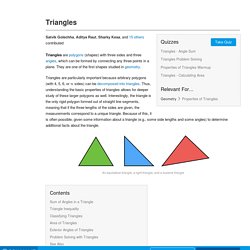
Here are some example questions that can be solved using some of the divisibility rules above. Brilliant Math & Science Wiki. Relationship of side lengths and angles of a triangle. Relationship of sides to interior angles in a triangle In a triangle: The shortest side is always opposite the smallest interior angle The longest side is always opposite the largest interior angle Try this Drag the orange dots on the triangle below.
Recall that in a scalene triangle, all the sides have different lengths and all the interior angles have different measures. Brilliant Math & Science Wiki. Main article: Area of a Triangle When determining the area of a triangle, note that a triangle can be thought of as half of a parallelogram.
The following picture should make this point clear: Brilliant Math & Science Wiki. Complementary angles are angles that add together to make a right angle.
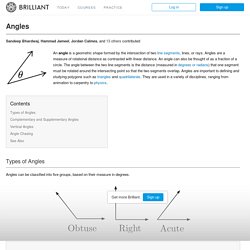
That is, and are complementary if Supplementary angles are angles that add together to make a straight line. That is, and are supplementary if In the image above, and are complementary, and and are supplementary. Angles and are complementary. Pythagorean Triples. A "Pythagorean Triple" is a set of positive integers, a, b and c that fits the rule: a2 + b2 = c2 Example: The smallest Pythagorean Triple is 3, 4 and 5. Let's check it: Calculating this becomes: And that is true Triangles. Properties of Triangles Lightning Quiz Practice Problems Online. Area of a Right Triangle Formula. Right angled triangle is a special type of triangle.
One of it's internal angle is a right angle. Geometry - About Perimeter - Circumference of Quarter Circle - Mathematics Stack Exchange. The Law of Sines. The Law of Sines (or Sine Rule) is very useful for solving triangles: a sin A = b sin B = c sin C It works for any triangle: And it says that:

Brilliant Math & Science Wiki. You can also generate the triples by using the formula abc=m2−1=2m=m2+1, where a2+b2=c2.
Brilliant Math & Science Wiki. Evaluate exactly.
Solution: Unit Circle with angle greater than 2 pi Notice that the problem reduces to finding the value of in the above picture. Since , makes an angle of with the negative -axis. SAT Practice Test Results. Math FAQ: Distance, Rate, and Time. The formula Distance = Rate x Time expresses one of the most frequently used relations in algebra.
Since an equation remains true as long as you divide through by the same non-zero element on each side, this formula can be written in different ways: To find rate, divide through on both sides by time: Distance Rate = ----------- Time Rate is distance (given in units such as miles, feet, kilometers, meters, etc.) divided by time (hours, minutes, seconds, etc.). Rate can always be written as a fraction that has distance units in the numerator and time units in the denominator, e.g., 25 miles/1 hour. To find time, divide through on both sides by rate: Distance Time = ----------- Rate When using this equation, it's important to keep the units straight. For instance, if the rate the problem gives is in miles per hour (mph), then the time needs to be in hours, and the distance in miles.
You can see why this is true if you look carefully at how the units are expressed. Back to the problem. Practice SAT Question Explanation. 10. In the figure above AD = 4, AB = 3 and CD = 9. What is the area of triangle AEC ? Correct Answer: D Explanation: If we take AE as the base of triangle AEC, then the height is CD.The height of the triangle is therefore, 9 (given).To find the base we need to see that triangles AEB and CDE are similar. Need more help with problem solving questions for the SAT? Practice SAT Question Explanation.