

Cancer modelling: Malignant maths. Tumor Model. With Jim Freyer, Jelena Pjesivac, Charles Cantrell, Kevin Flores, Zhiying Sun, Kejing He The microenvironment inside a tumor is extremely complex and adaptive, involving spatial and temporal variations in nutrient and waste gradients, cellular physiology, metabolism, the expression patterns of genes and proteins as well as the malignant progression.

The sum of all these elements defines the response of a tumor to treatment. The multicellular tumor spheroid system has been a primary example of in vitro models of the tumor microenvironment, which has provided numerous insights into tumor dynamics and progression. We develop a multiscale model to study spheroid tumor growth, which includes at the subcellular level a protein expression network that controls the possibility for cell cycle arrest, and at the cellular level a hybrid of cellular dynamics (lattice Monte Carlo) and reaction-diffusion dynamics of chemicals (PDEs). With Amy Bauer, Trachette Jackson with Lesette De Pillis.
Mathematical model of glioblastoma tumor spheroid. Learning the cell-graphs:Macroscopic modeling of brain tumors. Dynamics of a model for brain tumors window for intervention. In Silico Modeling of Brain Tumor Progression. Mathematical modeling of tumor growth reference list. Mathematical Models of Avascular Tumor Growth. Novel Tumor Growth Model. This work started as a result of a small grant from the National Institutes of Health Grant CA 84509.
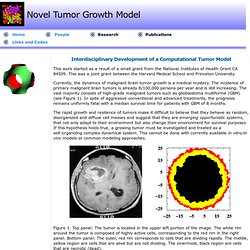
This was a joint grant between the Harvard Medical School and Princeton University. Currently, the dynamics of malignant brain tumor growth is a medical mystery. The incidence of primary malignant brain tumors is already 8/100,000 persons per year and is still increasing. The vast majority consists of high-grade malignant tumors such as glioblastoma multiforme (GBM) (see Figure 1). In spite of aggressive conventional and advanced treatments, the prognosis remains uniformly fatal with a median survival time for patients with GBM of 8 months. The rapid growth and resilience of tumors make it difficult to believe that they behave as random, disorganized and diffuse cell masses and suggest that they are emerging opportunistic systems, that not only adapt to their environment but also change their environment for survival purposes.
Figure 1. Publications: A. References: J. Reference: S. Y. Y. Virtual and real brain tumors using-mathematical-modeling-to-quantify-glioma-growth-and-invasion. Angiogenesis and tumor modeling. Malignant solid tumors generally are described as masses of tissue formed as a result of abnormal and excessive proliferation of mutant (atypical) cells, whose division has escaped the mechanisms that control normal cellular proliferation.

This abnormal proliferation of atypical cells in time leads to an uncontrolled growth, extending to the adjacent surrounding tissues, infiltrating and invading them; this invasion is local at first-causing primary tumors, but malignant cells have the ability of migrating through the blood vessels and/or the lymphatic system towards other parts of the body, giving rise to secondary tumors; this process is called metastasis and it is the one responsible for the host death. There are different stages of a malignant tumor evolution; described roughly, the main stages are the cellular stage and the macroscopic stage. Numerical Simulations We built a numerical simulation of a model for angiogenesis and tumor growth first proposed by De Angelis and Preziosi.
Mathematical models the mass effect of invasive brain tumors. Asymetric Cell Division. Projects:TumorModeling - NAMIC. From NAMIC Back to NA-MIC Collaborations, MIT Algorithms We are interested in developing computational methods for the assimilation of magnetic resonance image data into physiological models of glioma - the most frequent primary brain tumor - for a patient-adaptive modeling of tumor growth.
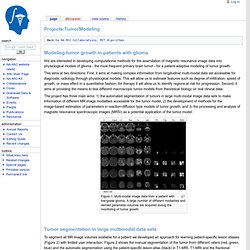
This aims at two directions: First, it aims at making complex information from longitudinal multi-modal data set accessible for diagnostic radiology through physiological models. This will allow us to estimate features such as degree of infiltration, speed of growth, or mass effect in a quantitative fashion; for therapy it will allow us to identify regions at risk for progression. Second, it aims at providing the means to test different macroscopic tumor models from theoretical biology on real clinical data. Figure 1: Multi-modal image data from a patient with low-grade glioma. Figure 2: Tumor segmentation - by human rater (red, green, blue) and our methods (black).