

Pi. Π Liczba π z dokładnością do 200 miejsc po przecinku: π ≈ 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196...[1] Niewymierność i przestępność liczby π[edytuj | edytuj kod] Jeśli średnica koła = 1, jego obwód wynosi π.
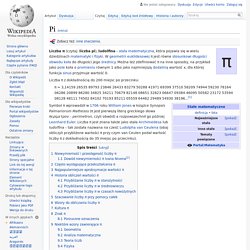
Liczba π jest liczbą niewymierną, co oznacza, że nie może być zapisana jako iloraz dwóch liczb całkowitych. Przybliżona konstrukcja Kochańskiego To ostatecznie rozstrzyga, że niemożliwa jest klasyczna konstrukcja (wyłącznie przy pomocy linijki i cyrkla) kwadratu o powierzchni równej powierzchni danego koła, gdyż współrzędne wszystkich punktów, które mogą być skonstruowane w taki sposób, należą do zbioru liczb nazywanych liczbami algebraicznymi. Dowód niewymierności π Ivana Nivena[2][edytuj | edytuj kod] Dowód przez sprowadzenie do sprzeczności.
Oraz Ponieważ wielomian n! Obliczanie liczby pi. Panopticum- strona główna Liczba π (inaczej ludolfina - od imienia holenderskiego matematyka Ludolfa van Ceulena, 1539-1610) określa stosunek długości obwodu koła do długości jego średnicy.
Jest to liczba niewymierna i w praktyce operujemy tylko jej, mniej lub bardziej dokładnym, przybliżeniem, np.: Gdyby dla kogoś było to za mało dokładnie, to stąd może ściągnąć plik tekstowy zawierający dokładniejsze przybliżenie : 500 tysięcy cyfr po przecinku. Liczbę π można przedstawić za pomocą sumy szeregu nieskończonego lub iloczynu nieskończonego. A). czyli: Wzór ten, odkryty przez Leibniza, otrzymuje się po rozwinięciu w szereg Maclaurina funkcji y = arctg x i podstawieniu x = 1 ( arctg 1 = π/4 ). B). czyli: To także rozwinięcie w szereg Maclaurina, ale tym razem funkcji y = arcsin x ( arcsin 1 = π/2 ).
C). D). czyli: To rozwinięcie, odkryte przez Eulera, otrzymuje się z teorii tzw. szeregów trygonometrycznych. E). czyli: Tutaj również skorzystano z szeregów trygonometrycznych. F). To było oczywiste. Π - liczba Pi (Ludolfina) Jak obliczyć liczbę ? Next: Pi-ematy, czyli jak zapamiętać Up: Liczby rzeczywiste Previous: Ułamek 0,(9) Już Archimedes (ok. 287 - 212 pne.)

OBLICZYŁ, że czyli a zatem OBLICZYŁ z dokładnością do dwóch miejsc dziesiętnych po przecinku. . , czyli z błędem mniejszym od 10-1000. Najbardziej znaczącym osiągnieciem w zakresie bezpośredniego porównywania koła z wielokątem było użycie przez Ludolfa van Ceulen (1540 - 1610), w 1582 r., wielokąta foremnego o 235 bokach, co pozwoliło wyznaczyć 20 dokładnych cyfr rozwinięcia dziesiętnego liczby. . , począwszy od szeregu Leibniza z 1673 r opublikowanego w 1682 r. w "Acta Eruditorum". Programiki, które NAPRAWDĘ liczą (procedury do obliczania z dowolną dokładnością) nie korzystają z rozwinięć dziesiętnych liczb wymiernych, tylko z szeregów potęgowych.
Przybliża z błędem mniejszym, niż 1/(kwadrat mianownika), a ostatni z tych ułamków gwarantuje, że żaden użytkownik kalkulatora w życiu nie natrafi na niedokładność. Liczbami wymiernymi nie może mieć "absolutnej" dokładności, bo liczba ? Monte Carlo – wyznaczamy przybliżenie liczby Pi / Programowanie / Artykuły / IT PWN - IT.PWN.PL. Przybliżanie wartości liczby Pi za pomocą metody Monte Carlo, to dobrze znany przykład, który bardzo dobrze oddaje sposób w jaki zazwyczaj przeprowadza się obliczenia typu Monte Carlo.
Wbrew pozorom, łatwo dokonać implementacji tej metody, nawet dla początkującego programisty jest to zadanie do zrealizowania w jeden przysłowiowy wieczór. Warto też dodać, iż sposób obliczenia przybliżenia liczby Pi, pozwala także na dość łatwe podanie implementacji, gdzie można wykorzystać możliwości programowania równoległego, jednak na początek warto zrobić tzw. wersję szeregową, gdzie obliczenia będą wykonywane przez jeden procesor, a dokładniej mówiąc przez jeden rdzeń obliczeniowy tego procesora. Takie rozwiązanie będzie równie proste, a dodatkowo później będziemy mogli je ulepszyć i sprawdzić na ile nasze ulepszenia np.: skróciły czas obliczeń. Nasz program opracowany zostanie w języku C++, choć nie będziemy korzystać z klas czy obiektów.
Młotek i dłuto, tj. kompilator, środowisko IDE i TinyMT. Liczba pi – Zmagania z ludolfiną. Kategorie: Powszechna, Starożytność, Nowożytność, XIX wiek, XX i XXI wiek, Historia nauki 2012-03-14 13:50 Wojciech Andryszek Trudno wyobrazić sobie naszą cywilizację bez liczby pi.
Ta matematyczna stała jest obecna w wielu dziedzinach naszego życia. Często stanowi fundamentalny element ważnych praw i zagadnień, które pozwala opisać w elegancki sposób. I choćby dlatego od 1988 roku 14 marca obchodzimy międzynarodowy Dzień Liczby π. Chyba wszyscy pamiętamy lekcje matematyki, na których z werwą lub przerażeniem liczyliśmy pole i obwód koła, objętość walca i stożka lub wodziliśmy wzrokiem za wykresami sinusów i cosinusów. Oczywiście ktoś, kto ma w sobie nieco rzymskiej, praktycznej duszy, chętniej złapałby za sznurek lub miarkę i bez problemu podał obwód wybranego słupa lub opony.
Początki. PREZENTACJAPT.LICZBAPI. Egipt PI.