

Information theory. Probability theory. As a mathematical foundation for statistics, probability theory is essential to many human activities that involve quantitative analysis of large sets of data.
Methods of probability theory also apply to descriptions of complex systems given only partial knowledge of their state, as in statistical mechanics. A great discovery of twentieth century physics was the probabilistic nature of physical phenomena at atomic scales, described in quantum mechanics. History[edit] The mathematical theory of probability has its roots in attempts to analyze games of chance by Gerolamo Cardano in the sixteenth century, and by Pierre de Fermat and Blaise Pascal in the seventeenth century (for example the "problem of points"). Christiaan Huygens published a book on the subject in 1657[2] and in the 19th century a big work was done by Laplace in what can be considered today as the classic interpretation.[3] This culminated in modern probability theory, on foundations laid by Andrey Nikolaevich Kolmogorov. . Measure (mathematics)
Informally, a measure has the property of being monotone in the sense that if A is a subset of B, the measure of A is less than or equal to the measure of B.
Furthermore, the measure of the empty set is required to be 0. Measure theory was developed in successive stages during the late 19th and early 20th centuries by Émile Borel, Henri Lebesgue, Johann Radon and Maurice Fréchet, among others. Probability space. A probability space consists of three parts: An outcome is the result of a single execution of the model.
Since individual outcomes might be of little practical use, more complex events are used to characterize groups of outcomes. Sample space. For example, if the experiment is tossing a coin, the sample space is typically the set {head, tail}.
For tossing two coins, the corresponding sample space would be {(head,head), (head,tail), (tail,head), (tail,tail)}. For tossing a single six-sided die, the typical sample space is {1, 2, 3, 4, 5, 6} (in which the result of interest is the number of pips facing up).[2] Multiple sample spaces[edit] Equally likely outcomes[edit] Up or down? In some sample spaces, it is reasonable to estimate or assume that all outcomes in the space are equally likely (that they occur with equal probability). Though most random phenomena do not have equally likely outcomes, it can be helpful to define a sample space in such a way that outcomes are at least approximately equally likely, since this condition significantly simplifies the computation of probabilities for events within the sample space.
Simple random sample[edit] Infinitely large sample spaces[edit] See also[edit] References[edit] Sigma-algebra. If X = {a, b, c, d}, one possible σ-algebra on X is Σ = {∅, {a, b}, {c, d}, {a, b, c, d}}, where ∅ is the empty set.
However, a finite algebra is always a σ-algebra. If {A1, A2, A3, …} is a countable partition of X then the collection of all unions of sets in the partition (including the empty set) is a σ-algebra. A more useful example is the set of subsets of the real line formed by starting with all open intervals and adding in all countable unions, countable intersections, and relative complements and continuing this process (by transfinite iteration through all countable ordinals) until the relevant closure properties are achieved (a construction known as the Borel hierarchy).
Motivation[edit] There are at least three key motivators for σ-algebras: defining measures, manipulating limits of sets, and managing partial information characterized by sets. Measure[edit] One would like to assign a size to every subset of X, but in many natural settings, this is not possible. Observe that then or. Probability measure. Intuitively, the additivity property says that the probability assigned to the union of two disjoint events by the measure should be the sum of the probabilities of the events, e.g. the value assigned to "1 or 2" in a throw of a die should be the sum of the values assigned to "1" and "2".
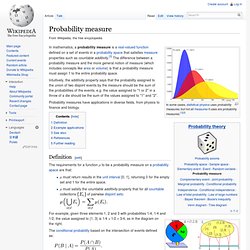
Probability measures have applications in diverse fields, from physics to finance and biology. Definition[edit] A probability measure mapping the probability space for 3 events to the unit interval. Stochastic process. Stock market fluctuations have been modeled by stochastic processes.
In probability theory, a stochastic process /stoʊˈkæstɪk/, or sometimes random process (widely used) is a collection of random variables; this is often used to represent the evolution of some random value, or system, over time. This is the probabilistic counterpart to a deterministic process (or deterministic system). Instead of describing a process which can only evolve in one way (as in the case, for example, of solutions of an ordinary differential equation), in a stochastic or random process there is some indeterminacy: even if the initial condition (or starting point) is known, there are several (often infinitely many) directions in which the process may evolve. Formal definition and basic properties[edit]