

Cauchy distribution. The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution.
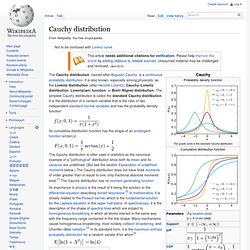
It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. List of probability distributions. Many probability distributions are so important in theory or applications that they have been given specific names.
Discrete distributions[edit] With finite support[edit] With infinite support[edit] Continuous distributions[edit] Supported on a bounded interval[edit] Supported on semi-infinite intervals, usually [0,∞)[edit] Supported on the whole real line[edit] With variable support[edit] Stable distribution. The importance of stable probability distributions is that they are "attractors" for properly normed sums of independent and identically-distributed (iid) random variables.

The normal distribution is one family of stable distributions. By the classical central limit theorem the properly normed sum of a set of random variables, each with finite variance, will tend towards a normal distribution as the number of variables increases. Without the finite variance assumption the limit may be a stable distribution. Stable distributions that are non-normal are often called stable Paretian distributions,[citation needed] after Vilfredo Pareto. q-analogs of all symmetric stable distributions have been defined, and these recover the usual symmetric stable distributions in the limit of q → 1.[1] Normal distribution. In probability theory, the normal (or Gaussian) distribution is a very commonly occurring continuous probability distribution—a function that tells the probability that an observation in some context will fall between any two real numbers.
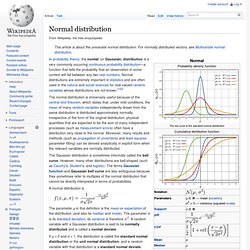
Normal distributions are extremely important in statistics and are often used in the natural and social sciences for real-valued random variables whose distributions are not known.[1][2] The normal distribution is immensely useful because of the central limit theorem, which states that, under mild conditions, the mean of many random variables independently drawn from the same distribution is distributed approximately normally, irrespective of the form of the original distribution: physical quantities that are expected to be the sum of many independent processes (such as measurement errors) often have a distribution very close to the normal. Lévy distribution. Yule–Simon distribution. In probability and statistics, the Yule–Simon distribution is a discrete probability distribution named after Udny Yule and Herbert A.
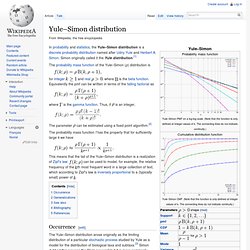
Simon. Generalized extreme value distribution. In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions.
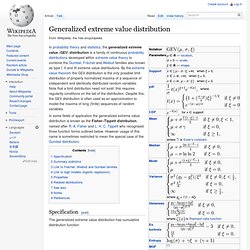
Gumbel distribution. In probability theory and statistics, the Gumbel distribution is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions.

Such a distribution might be used to represent the distribution of the maximum level of a river in a particular year if there was a list of maximum values for the past ten years. It is useful in predicting the chance that an extreme earthquake, flood or other natural disaster will occur. Gompertz function. A Gompertz curve or Gompertz function, named after Benjamin Gompertz, is a sigmoid function.
It is a type of mathematical model for a time series, where growth is slowest at the start and end of a time period. The right-hand or future value asymptote of the function is approached much more gradually by the curve than the left-hand or lower valued asymptote, in contrast to the simple logistic function in which both asymptotes are approached by the curve symmetrically. It is a special case of the generalised logistic function.
Formula[edit] where Differentiation[edit] The function curve can be derived from a Gompertz law of mortality, which states the rate of mortality (decay) falls exponentially with current size. Is the rate of growth.k is an arbitrary constant. Example uses[edit] Examples of uses for Gompertz curves include: Growth of tumors[edit] In the 1960s A.K. Where: independently on X(0)>0. Α is a constant related to the proliferative ability of the cells.log() refers to the natural log.