

Metric space. The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space.
In fact, the notion of "metric" is a generalization of the Euclidean metric arising from the four long-known properties of the Euclidean distance. The Euclidean metric defines the distance between two points as the length of the straight line segment connecting them. Other metric spaces occur for example in elliptic geometry and hyperbolic geometry, where distance on a sphere measured by angle is a metric, and the hyperboloid model of hyperbolic geometry is used by special relativity as a metric space of velocities. A metric space also induces topological properties like open and closed sets which leads to the study of even more abstract topological spaces.
History[edit] Maurice Fréchet introduced metric spaces in his work Sur quelques points du calcul fonctionnel, Rendic. Definition[edit] A metric space is an ordered pair where is a set and such that for any about. Cauchy sequence. Shown in blue, as versus If the space containing the sequence is complete, the "ultimate destination" of this sequence (that is, the limit) exists.
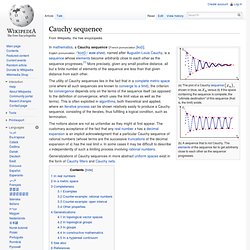
The notions above are not as unfamiliar as they might at first appear. The customary acceptance of the fact that any real number x has a decimal expansion is an implicit acknowledgment that a particular Cauchy sequence of rational numbers (whose terms are the successive truncations of the decimal expansion of x) has the real limit x. In some cases it may be difficult to describe x independently of such a limiting process involving rational numbers. Generalizations of Cauchy sequences in more abstract uniform spaces exist in the form of Cauchy filters and Cauchy nets.
In real numbers[edit] A sequence of real numbers is called a Cauchy sequence, if for every positive real number ε, there is a positive integer N such that for all natural numbers m, n > N where the vertical bars denote the absolute value. In a metric space[edit] and Completeness[edit]
Octonions. Next: Introduction The octonions are the largest of the four normed division algebras.

While somewhat neglected due to their nonassociativity, they stand at the crossroads of many interesting fields of mathematics. Here we describe them and their relation to Clifford algebras and spinors, Bott periodicity, projective and Lorentzian geometry, Jordan algebras, and the exceptional Lie groups. We also touch upon their applications in quantum logic, special relativity and supersymmetry. Table of Contents: This website also contains a lot of extra material on the octonions: Octonions online links to other websites containing material about the octonions.
For a lighter approach, try this two-part feature in Plus Magazine: Curious quaternions and Ubiquitous octonions in which Helen Joyce and I have a fun nontechnical chat about the real numbers, complex numbers, quaternions and octonions. John Baez and John Huerta, G2 and the rolling ball. . © 2016 John Baez baez@math.removethis.ucr.andthis.edu.
Real / Functional Analysis Video Lectures? For Lebesgue, I suggest Stein and Shakarchi's book Real Analysis which also goes through Hilbert Spaces and their many examples. Royden's Real Analysis is also very good. Rudin has two small chapter introducing Lebesgue integration and differential forms in his Principles of Mathematical Analysis. Rudin also goes through all the necessary things on metric spaces. This is the standard text in introductory analysis classes. Rudin also has a book on Functional Analysis but I prefer Conway's. For differential forms and calculus on manifolds, Munkres has a book on Analysis on Manifolds. Real analysis.