

Merkaba, Platonic Solids & Sacred Geometry. The MerKaBa The Merkaba is an extremely powerful symbol.
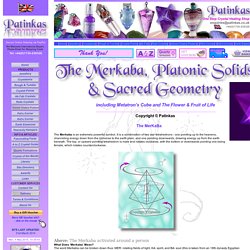
It is a combination of two star tetrahedrons - one pointing up to the heavens, channeling energy down from the Universe to the earth plain, and one pointing downwards, drawing energy up from the earth beneath. The top, or upward pointing tetrahedron is male and rotates clockwise, with the bottom or downwards pointing one being female, which rotates counterclockwise. Above: The Merkaba activated around a person What Does ‘Merkaba’ Mean? What is a Merkaba? When meditating, try sitting holding a MerKaBa and picture yourself inside this shape, with the two tetrahedrons rotating (as described above). Platonic Solids and Sacred Geometry Above: The 5 Platonic Solids Platonic Solids are shapes which form part of Sacred Geometry.
They are made up of the 'Five Convex Regular Polyhedra': hexahedron (cube), octahedron (double inverted pyramid), tetrahedron (pyramid), Icosohedron and dodecahedron. Flower of Life Above: The Flower of Life back to top. SGDS: Free Samples. The Geometry Code:Universal Symbolic Mirrors of Natural Laws Within Us Sacred Geometry Resources, Books, Art Prints, Cards, Screensavers, Videos, Patterns, Blog and more You are here: Home / Store / Sacred Geometry Books / Sacred Geometry Design Sourcebook (SGDS) / SGDS: Free Samples SGDS: Free Samples Free Samples Please note the copyright info on the FAQ page for these items. Free Patterns from Sacred Geometry Design SourceBook – Universal Dimensional Patterns by Bruce Rawles Sample pages from Sacred Geometry Design SourceBook – Universal Dimensional Patterns by Bruce Rawles Sample pages from Sacred Geometry Design SourceBook (including both text and graphics) NEW! Platonic Solid Foldup Patterns Platonic Solid Foldup Patterns (downloadable pdf file with all 5 patterns) Individual Platonic Solid Fold-up Patterns Archimedean Solid Foldup Patterns Archimedean Solid Foldup Patterns (downloadable pdf file with all 13 patterns) Individual Archimedean Solid Fold-up Patterns Other Patterns and Designs.
Sacred Geometry Design Sourcebook – bonus page – Kepler’s Solid. <A HREF=" Widgets</A> Amazon.com - an ever-growing list of books, videos, tools, software, art and other items, or just select from the entire Amazon site Astro-logix - a unique system of glow-in-the-dark hubs and day-glow cylinders to make a phenomenal variety of 2D and 3D geometric models Bluehost - our GeometryCode.com webhost and domain registrar offers superb customer service, technical expertise and value; tops in every respect!

Crop Circle Oracle Cards - A deck of 80 splendid geometric patterns made with cereal grains, photographed by leading researchers, Kabbalistic interpretations by Joseph-Mark Cohen Flying Cat Travel - Visiting the Great Pyramid, the Parthenon or some other geometrically interesting place? Fractiles - Versatile geometric toys made of magnetic diamond shaped tiles Gaiam - Products for sustainable, interconnected living Heartmath - Biofeedback using the heart's mathematics of interconnection. Origami - MM's Modular Mania. Paper-model.com - Home of PaperCut software for paper model construction.
Platonic. If you have a slow internet connection try this version instead.

John Baez November 12, 2006 What's the pattern in this sequence? Infinity, five, six, three, three, three, three, three, ... In 2 dimensions, the most symmetrical polygons of all are the 'regular polygons'. In 3 dimensions, the most symmetrical polyhedra of all are the 'regular polyhedra', also known as the 'Platonic solids'. The tetrahedron, with 4 triangular faces: The cube, with 6 square faces: The octahedron, with 8 triangular faces: The dodecahedron, with 12 pentagonal faces. The story goes on... but in higher dimensions one usually uses the term 'regular polytopes' instead of 'Platonic solids'. In 4 dimensions, there are exactly six regular polytopes. How can visualize these? So, we can visualize the regular polytopes in 4 dimensions by taking a 3-sphere and drawing it chopped up into polyhedra.
You might things would keep getting more complicated in higher dimensions. For starters, try Tony Smith's webpage. Hmm.