

Knapsack problem. Example of a one-dimensional (constraint) knapsack problem: which boxes should be chosen to maximize the amount of money while still keeping the overall weight under or equal to 15 kg?
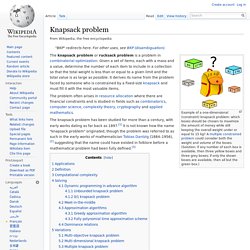
A multiple constrained problem could consider both the weight and volume of the boxes. (Answer: if any number of each box is available, then three yellow boxes and three grey boxes; if only the shown boxes are available, then all but the green box.) The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a mass and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items. Applications[edit] Definition[edit] Mathematically the 0-1-knapsack problem can be formulated as: Let there be items, to. Travelling salesman problem.
The travelling salesman problem (TSP) asks the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?
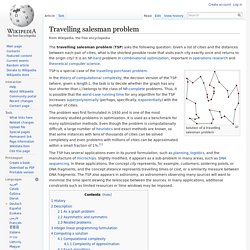
It is an NP-hard problem in combinatorial optimization, important in operations research and theoretical computer science. Solution of a travelling salesman problem TSP is a special case of the travelling purchaser problem. In the theory of computational complexity, the decision version of the TSP (where, given a length L, the task is to decide whether the graph has any tour shorter than L) belongs to the class of NP-complete problems. Thus, it is possible that the worst-case running time for any algorithm for the TSP increases superpolynomially (perhaps, specifically, exponentially) with the number of cities. The problem was first formulated in 1930 and is one of the most intensively studied problems in optimization. History[edit] Richard M. Since For are. Boolean satisfiability problem. SAT was the first known example of an NP-complete problem.
That briefly means that there is no known algorithm that efficiently solves all instances of SAT, and it is generally believed (but not proven, see P versus NP problem) that no such algorithm can exist. Further, a wide range of other naturally occurring decision and optimization problems can be transformed into instances of SAT. A class of algorithms called SAT solvers can efficiently solve a large enough subset of SAT instances to be useful in various practical areas such as circuit design and automatic theorem proving, by solving SAT instances made by transforming problems that arise in those areas. Extending the capabilities of SAT solving algorithms is an ongoing area of research. However, no current such methods can efficiently solve all SAT instances. Basic definitions and terminology[edit] Complexity and restricted versions[edit] Unrestricted satisfiability (SAT)[edit] 3-satisfiability[edit] Exactly-1 3-satisfiability[edit]
Halting problem. Alan Turing proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist.
A key part of the proof was a mathematical definition of a computer and program, which became known as a Turing machine; the halting problem is undecidable over Turing machines. It is one of the first examples of a decision problem. Jack Copeland (2004) attributes the term halting problem to Martin Davis.[1] Background[edit] The halting problem is a decision problem about properties of computer programs on a fixed Turing-complete model of computation, i.e. all programs that can be written in some given programming language that is general enough to be equivalent to a Turing machine.
For example, in pseudocode, the program: while (true) continue does not halt; rather, it goes on forever in an infinite loop. Print "Hello, world! " does halt. While deciding whether these programs halt is simple, more complex programs prove problematic. Representation as a set[edit]