

Sorting. Problems. P ?= NP. Divide and conquer algorithms. In computer science, divide and conquer (D&C) is an important algorithm design paradigm based on multi-branched recursion.
A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same (or related) type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem. This technique is the basis of efficient algorithms for all kinds of problems, such as sorting (e.g., quicksort, merge sort), multiplying large numbers (e.g. Karatsuba), syntactic analysis (e.g., top-down parsers), and computing the discrete Fourier transform (FFTs). On the other hand, the ability to understand and design D&C algorithms is a skill that takes time to master.
The correctness of a divide and conquer algorithm is usually proved by mathematical induction, and its computational cost is often determined by solving recurrence relations. Decrease and conquer[edit] items. Randomized algorithm. One has to distinguish between algorithms that use the random input to reduce the expected running time or memory usage, but always terminate with a correct result (Las Vegas algorithms) in a bounded amount of time, and probabilistic algorithms, which, depending on the random input, have a chance of producing an incorrect result (Monte Carlo algorithms) or fail to produce a result either by signalling a failure or failing to terminate.
In the second case, random performance and random output, the term "algorithm" for a procedure is somewhat questionable. In the case of random output, it is no longer formally effective.[1] However, in some cases, probabilistic algorithms are the only practical means of solving a problem.[2] In common practice, randomized algorithms are approximated using a pseudorandom number generator in place of a true source of random bits; such an implementation may deviate from the expected theoretical behavior.
Motivation[edit] Output: Find an ‘a’ in the array. . Master theorem. In the analysis of algorithms, the master theorem provides a cookbook solution in asymptotic terms (using Big O notation) for recurrence relations of types that occur in the analysis of many divide and conquer algorithms.
It was popularized by the canonical algorithms textbook Introduction to Algorithms by Cormen, Leiserson, Rivest, and Stein, in which it is both introduced and proved. Not all recurrence relations can be solved with the use of the master theorem; its generalizations include the Akra–Bazzi method. Introduction[edit] Consider a problem that can be solved using a recursive algorithm such as the following: procedure T( n : size of problem ) defined as: if n < 1 then exit Do work of amount f(n) Greedy algorithm. Greedy algorithms determine minimum number of coins to give while making change.
These are the steps a human would take to emulate a greedy algorithm to represent 36 cents using only coins with values {1, 5, 10, 20}. The coin of the highest value, less than the remaining change owed, is the local optimum. (Note that in general the change-making problem requires dynamic programming or integer programming to find an optimal solution; However, most currency systems, including the Euro and US Dollar, are special cases where the greedy strategy does find an optimum solution.) For example, a greedy strategy for the traveling salesman problem (which is of a high computational complexity) is the following heuristic: "At each stage visit an unvisited city nearest to the current city".
This heuristic need not find a best solution but terminates in a reasonable number of steps; finding an optimal solution typically requires unreasonably many steps. Specifics[edit] Greedy choice property Types[edit] Dynamic programming. In mathematics, computer science, economics, and bioinformatics, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems.
It is applicable to problems exhibiting the properties of overlapping subproblems[1] and optimal substructure (described below). When applicable, the method takes far less time than naive methods that don't take advantage of the subproblem overlap (like depth-first search). The idea behind dynamic programming is quite simple. Linear programming. A pictorial representation of a simple linear program with two variables and six inequalities.
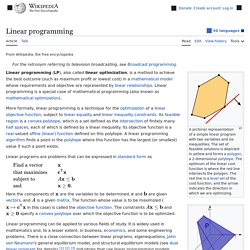
The set of feasible solutions is depicted in yellow and forms a polygon, a 2-dimensional polytope. The linear cost function is represented by the red line and the arrow: The red line is a level set of the cost function, and the arrow indicates the direction in which we are optimizing. Linear programming (LP; also called linear optimization) is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming (mathematical optimization). Linear programs are problems that can be expressed in canonical form as.
Cache-oblivious algorithm. In computing, a cache-oblivious algorithm (or cache-transcendent algorithm) is an algorithm designed to take advantage of a CPU cache without having the size of the cache (or the length of the cache lines, etc.) as an explicit parameter.
An optimal cache-oblivious algorithm is a cache-oblivious algorithm that uses the cache optimally (in an asymptotic sense, ignoring constant factors). Thus, a cache oblivious algorithm is designed to perform well, without modification, on multiple machines with different cache sizes, or for a memory hierarchy with different levels of cache having different sizes. Cache-oblivious algorithms are contrasted with explicit blocking, as in loop nest optimization, which explicitly breaks a problem into blocks that are optimally sized for a given cache.
Optimal cache-oblivious algorithms are known for the Cooley–Tukey FFT algorithm, matrix multiplication, sorting, matrix transposition, and several other problems. History[edit] Idealized cache model[edit] . . And.