

Exact trigonometric constants. Exact algebraic expressions for trigonometric values are sometimes useful, mainly for simplifying solutions into radical forms which allow further simplification.
All values of the sines, cosines, and tangents of angles at 3° increments are derivable in radicals using identities—the half-angle identity, the double-angle identity, and the angle addition/subtraction identity—and using values for 0°, 30°, 36°, and 45°. Note that 1° = π/180 radians. According to Niven's theorem, the only rational values of the sine function for which the argument is a rational number of degrees are 0, 1/2, and 1. Fermat number[edit] The list in this article is incomplete in at least two senses.
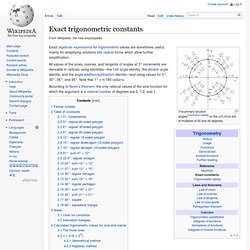
Table of constants[edit] Values outside the [0°, 45°] angle range are trivially derived from these values, using circle axis reflection symmetry. 0°: fundamental[edit] 3°: regular 60-sided polygon[edit] 6°: regular 30-sided polygon[edit] 9°: regular 20-sided polygon[edit] 12°: regular 15-sided polygon[edit] (Silver ratio) Thus. Wythoff construction. Wythoffian constructions from 3 mirrors forming a right triangle.
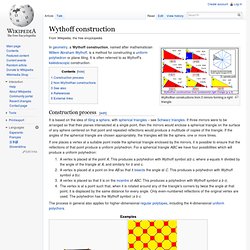
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction. Construction process[edit] It is based on the idea of tiling a sphere, with spherical triangles – see Schwarz triangles. If three mirrors were to be arranged so that their planes intersected at a single point, then the mirrors would enclose a spherical triangle on the surface of any sphere centered on that point and repeated reflections would produce a multitude of copies of the triangle. If one places a vertex at a suitable point inside the spherical triangle enclosed by the mirrors, it is possible to ensure that the reflections of that point produce a uniform polyhedron. A vertex is placed at the point A. Non-Wythoffian constructions[edit] See also[edit] ENCYCLOPEDIA OF TRIANGLE CENTERS. X(585) = 1st CONGRUENT SHRUNK INSQUARES POINT Trilinears f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = [2*area*(1/b + 1/c - 1/a) + b + c - a]/a Barycentrics g(a,b,c) : g(b,c,a) : g(c,a,b), where g(a,b,c) = 2*area*(1/b + 1/c - 1/a) + b + c - a X(585) lies on this line: 8,192 For a discussion, see Floor van Lamoen, "Vierkanten in een driehoek: 5.

Gekrompen ingeschreven vierkanten" X(586) = 2nd CONGRUENT SHRUNK INSQUARES POINT Trilinears f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = [2*area*(1/b + 1/c - 1/a) + a - b - c]/a Barycentrics g(a,b,c) : g(b,c,a) : g(c,a,b), where g(a,b,c) = 2*area*(1/b + 1/c - 1/a) + a - b - c. Coxeter–Dynkin diagram. Coxeter–Dynkin diagrams for the fundamental finite Coxeter groups Coxeter–Dynkin diagrams for the fundamental affine Coxeter groups Each diagram represents a Coxeter group, and Coxeter groups are classified by their associated diagrams.
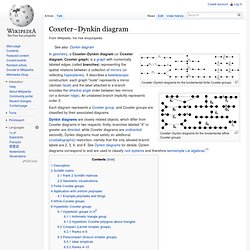
Dynkin diagrams are closely related objects, which differ from Coxeter diagrams in two respects: firstly, branches labeled "4" or greater are directed, while Coxeter diagrams are undirected; secondly, Dynkin diagrams must satisfy an additional (crystallographic) restriction, namely that the only allowed branch labels are 2, 3, 4, and 6. See Dynkin diagrams for details. Dynkin diagrams correspond to and are used to classify root systems and therefore semisimple Lie algebras.[1] Description[edit] Branches of a Coxeter–Dynkin diagram are labeled with a rational number p, representing a dihedral angle of 180°/p. Diagrams can be labeled by their graph structure. Schläfli matrix[edit] Finite and affine groups are also called elliptical and parabolic respectively.