

L'organisation en rhombes - TPE Les alvéoles d'abeilles. Pour mener à bien cette étude, nous ne considèrerons qu'un alvéole.
On ne s’interesse dans cette démonstration qu'uniquement à un tier du prisme originel composant l'alvéole d'abeille.. Nous tenterons de montrer les différences entre l'organisation spécifique des abeilles (en rhombes) et l'utilisation de prisme complet classique. Hypothèse. Physique de tous les jours. « Ce qui distingue d’emblée le pire architecte de l’abeille la plus experte, c’est qu’il a construit la cellule dans sa tête avant de la construire dans la ruche. » Karl Marx Si Karl Marx oppose « le pire à architecte » à l’abeille ouvrière, c’est qu’il a été fasciné par la géométrie de leurs ruches.
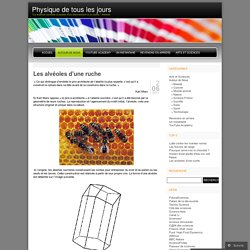
Lois physiques:1 Abeilles: 0. La régularité extraordinaire des nids d’abeille est l’une des curiosités naturelles qui a le plus excité les esprits.
Par exemple, le mathématicien Pappus d’Alexandrie avait remarqué dès l’Antiquité que ces structures hexagonales permettaient aux abeilles d’aménager le maximum d’alvéoles pour un minimum de cire. En ce jour de rentrée, voilà de quoi rendre jaloux les cancres en maths. Comment ces petits bêtes n’ayant pas deux grammes de cervelle peuvent-elles élaborer des constructions aussi optimales qu’élégantes? L'âme de géomètre des abeilles. Les abeilles ont-elles une âme géométrique pour construire leurs nids optimisés ?
David Parker/SPL/Cosmos Alain SATABIN est professeur de mathématiques au lycée Gaspard Monge de Charleville-Mézières. De toutes les structures hexagonales, la plus connue et, sans doute, l'une des plus belles, est celle des alvéoles que construisent les abeilles. D'Arcy Thompson Une fleur de tournesol, un chou romanesco ou une toile d'araignée sont autant d'exemples dont la géométrie ne laisse pas indifférents les mathématiciens : la nature leur offre ainsi de nombreuses sources d'inspiration pour échafauder théories et modèles. Du théorème du nid d’abeille à la conjecture de Kelvin. En mathématiques, il existe quelques problèmes très simples à énoncer mais incroyablement difficiles à résoudre.

C’est particulièrement vrai en arithmétique, et j’ai déjà eu l’occasion d’écrire des billets sur la conjecture de Goldbach (ici) et sur celle de Syracuse (là). Aujourd’hui, nous allons voir qu’en géométrie aussi, il existe des conjectures qu’un collégien peut comprendre mais sur lesquelles les meilleurs mathématiciens du monde se cassent les dents. Et comme la géométrie est partout autour de nous, cela va nous permettre de faire un tour dans le monde des abeilles et celui des bulles de savon. Un problème de pavage C’est décidé, vous allez refaire le carrelage de votre cuisine ! Le webinet des curiosités: Lois physiques:1 Abeilles: 0. La régularité extraordinaire des nids d'abeille est l'une des curiosités naturelles qui a le plus excité les esprits.
Par exemple, le mathématicien Pappus d'Alexandrie avait remarqué dès l'Antiquité que ces structures hexagonales permettaient aux abeilles d'aménager le maximum d'alvéoles pour un minimum de cire. En ce jour de rentrée, voilà de quoi rendre jaloux les cancres en maths. Comment ces petits bêtes n'ayant pas deux grammes de cervelle peuvent-elles élaborer des constructions aussi optimales qu'élégantes? Deux mille ans plus tard, les fausses explications ont toujours la vie dure... Collège Jacques Monod - Le Konacker - HAYANGE. Sources : Curiosités géométriques, Emile Fourrey, Librairie Vuibert, 1907.
Les ouvrières butineuses parcourent parfois plusieurs kilomètres pour récolter les ressources nécessaires (le nectar, le pollen, la propolis et l'eau) à la colonie. Les jeunes ouvrières transforment le nectar en miel. Les abeilles élèvent leurs jeunes et emmagasinent miel et pollen dans les alvéoles. L'ensemble des alvéoles constitue le rayon qui est un gâteau de cire fabriqué par les ouvrières.