

Atelier d'architecture / Maison « (1+√5)/2 », Dolni Bogrov - 5ko.fr. C'est la première maison réelle qui sera construite, et pour laquelle j'ai été projeteur en chef.

Aujourd'hui, le permis de construire a été délivré et la construction débutera bientôt. La maison se trouve à Dolni Bogrov, village dans la région de Sofia. Le bâtiment est nommé "Maison « (1+√5)/2 »" car le projet architectural -- plan, façades, toits, proportions -- est basé sur le nombre d'or. Vues 3D - croquis en perspective : Façades : Plan et coupes : Les clients sont un jeune couple sans enfants, tous les deux ingénieurs.
Au départ, ce n'est pas moi qui étais en charge de ce projet. J'ai commencé par « table rase », avec les quelques données de départ que j'avais. Bâtiment à un seul niveau, plancher principal sur-élevé par rapport au sol, un grand séjour avec cuisine intégrée et cheminée, un petit bureau de travail et de réception de collaborateurs, trois chambres. A un moment, les clients avaient utilisé l'expression « maison préhistorique sur pilotis ». Ma participation inclut : En architecture en en peinture. : TPE sur le nombre d'or et la suite de Fibonacci. On observe dans le monde antique, avant même l’apparition de la notion du nombre d’or, des apparitions de proportions proche du nombre d’or.
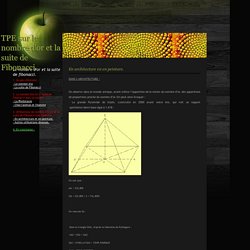
On peut ainsi évoquer : - La grande Pyramide de Gizeh, construite en 2000 avant notre ère, qui voit un rapport apothème/demi-base égal à 1.618 : On sait que : On cherche SA : Dans le triangle SOA, d'après le théorème de Pythagore : D'où, SA = 188,4546... On a alors le rapport : SA / OA = 188,4546 / 116,5025 = 1,617601... - Le parthénon, érigé au 5eme siècle avant notre ère et dont les têtes pensantes de la construction étaient Phidias (qui donnera le nom de Phi au nombre d’or) et Ictinos. La façade du Parthénon s'inscrit dans un rectangle d'or montré sur le dessin ci-dessous. (La hauteur est 134 pixels, et la largeur est de 217 pixels. La « divine proportion » refait véritablement surface durant la renaissance. Il optera bien souvent pour des constructions simples et géométriques, à la recherche des Proportions Parfaites.
L'architecture et le nombre d'or. Architecture. De tous temps, les Mathématiques ont été au service de l'Art.

Des pyramides d'Egypte aux temples grecs, de l'époque de la Renaissance avec Piero Del la Francesca, à nos jours, l'utilisation du nombre d'or a permis de réaliser de grands chefs d'oeuvres car il leur confère une esthétique des plus belles. L'art du XIXème siècle n'a pas échappé à cette recherche de la beauté et le peintre Sérusier en 1890 a défini un format idéal appelé La Porte d’Harmonie. Le nombre d’or est un rapport entre deux dimensions phi =1.618 Au XX ème siècle, de grands peintres, architectes et sculpteurs ont accompli leurs oeuvres en alliant l'Art et les Mathématiques. Dans cette partie du site nous vous proposons quelques exemples d'utilisation de phi dans l'architecture :
Le nombre d'or dans l'architecture grecque : mythe ou réalité ? Filles des nombres d’or, Fortes des lois du ciel, Sur nous tombe et s’endort, Un Dieu couleur de miel.
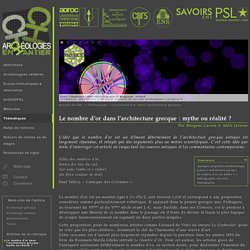
Paul Valéry, « Cantique des Colonnes ». Le nombre d’or est un nombre égal à (1+√5)/2, soit environ 1,618 et correspond à une proportion considérée comme particulièrement esthétique. Il apparaît dans la pensée grecque avec Pythagore, au tournant du VIème et du Vème siècle avant J. -C. mais Euclide, dans ses Eléments, est le premier à développer une théorie de ce nombre dans le passage où il tente de définir la façon la plus logique de couper harmonieusement un segment en deux parties inégales. Cette proportion, pour de nombreux artistes comme Léonard de Vinci ou encore Le Corbusier -pour ne citer que les plus célèbres-, donnerait la clef de l’harmonie d’une œuvre d’art.
Mais dans quelle mesure n’y a-t-il pas là un mythe architectural ? Quelques propriétés mathématiques La section d’or La célèbre suite de Fibonacci, mathématicien du XIIIème siècle, entretient des liens étroits avec φ.