

21 Incredible Math Art Projects for Kids. Sliceform Studio. How to wrap presents without tape or ribbon - origami-style. Mathematical Present Wrapping. How To Wrap A Present With Mathematical Precision (and Waste Less Paper) 13.1K 1736Share51 It's not hard to wrap a box if you don't care how much wrapping paper or tape you use, but what if you care about efficiency?
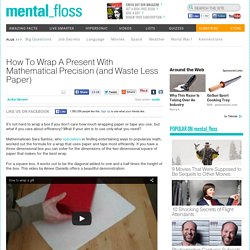
What if your aim is to use only what you need? Mathematician Sara Santos, who specializes in finding entertaining ways to popularize math, worked out the formula for a wrap that uses paper and tape most efficiently. If you have a three dimensional box you can solve for the dimensions of the two dimensional square of paper that makes for the best wrap. For a square box, it works out to be the diagonal added to one and a half times the height of the box. For a rectangular box, things get more complicated. Not only does the power of math let you optimize for paper and tape usage, it also lets you prettily match up the pattern on the wrapping paper where the edges meet. Now get out your rulers, spreadsheets, and calculators, and get to work on your most satisfyingly exact giftwrapping season ever! Templatemaker.nl.
Fun With Folding. After attending a brilliant MoMath talk on Mathematical Origami given by Erik Demaine, I have been folding, cutting, and taping more than I ever thought I would.
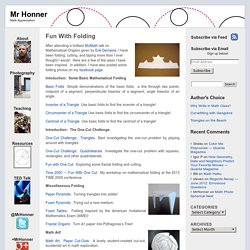
Here are a few of the ways I have been inspired. In addition, I have also posted some folding photos on my facebook page. Ask Dr. Math. Math Craft How-Tos « Wonder How To. Mathematics Awareness Month - April 2014 - Fold and One Cut. Navigate the Calendar.
Fun with Paper Folding. Over the last several years, I’ve been able to work with teachers from local school districts as part of a grant-funded project called “The Math and Science Partnership Program” (MSP).
Phase II of this program focuses on “Improving Math & Science Teaching through School Outreach.” We offer free professional development workshops for teachers, held on Saturdays, several times a year. Teachers who are part of our MSP Partner Schools can earn a $150 stipend from attending each workshop.
All workshops are accepted for re-certification credit in the Berkeley & Charleston County School districts. Fold and cut part 3. We decided to do one more fold and cut project tonight.
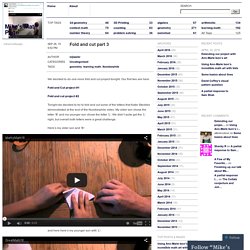
Our first two are here: Fold and Cut project #1 Fold and cut project #2 Tonight we decided to try to fold and cut some of the letters that Katie Steckles demonstrated at the end of the Numberphile video. My older son chose the letter ‘B’ and my younger son chose the letter ‘L’. Math for nine-year-olds: fold, punch and cut for symmetry! Today I had the pleasure to visit my daughter’s fourth-grade classroom for some fun mathematical activities.
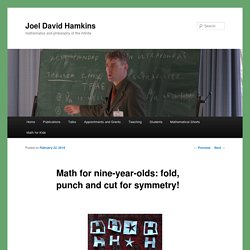
The topic was Symmetry! I planned some paper-folding activities, involving hole-punching and cutting, aiming to display the dynamism that is present in the concept of symmetry. Symmetry occurs when a figure can leap up, transforming itself through space, and land again exactly upon itself in different ways. I sought to have the students experience this dynamic action not only in their minds, as they imagined various symmetries for the figures we considered, but also physically, as they folded a paper along a line of symmetry, checking that this fold brought the figure exactly to itself.
The exercises were good plain fun, and some of the kids wanted to do them again and again, the very same ones. Next, we handled a few patterns that required two folds. The three-fold patterns are a bit more challenging, but almost all of the kids were able to do it. Fun With Folding. The Fold-and-Cut Problem (Erik Demaine) Problem What shapes can result from the following fold-and-cut process?
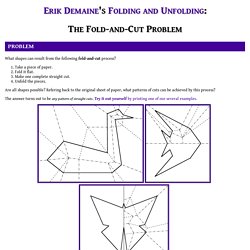
Take a piece of paper. Fold it flat. Make one complete straight cut. Unfold the pieces. The answer turns out to be any pattern of straight cuts. History The first published reference to folding and cutting of which we are aware is a Japanese book, Wakoku Chiyekurabe (Mathematical Contests), by Kan Chu Sen, published in 1721. Another early reference to folding and cutting is a July 1873 article “National Standards and Emblems” in Harper's New Monthly Magazine, volume 47, number 278. Before Houdini was a famous escape artist, he was a general magician. Another magician, Gerald Loe, studied the fold-and-cut idea in some detail. Martin Gardner wrote about the fold-and-cut problem in his famous series in Scientific American (“Paper cutting”, chapter 5 of New Mathematical Diversions (Revised Edition), Mathematical Association of America, Washington, D.C., 1995.).
Fold Your Way to Glory. Yesterday, I led a meeting of a Teachers’ Math Circle about the fold and cut theorem.
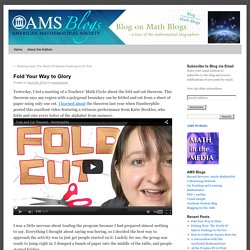
This theorem says any region with a polygonal boundary can be folded and cut from a sheet of paper using only one cut. I learned about the theorem last year when Numberphile posted this excellent video featuring a virtuoso performance from Katie Steckles, who folds and cuts every letter of the alphabet from memory. I was a little nervous about leading the program because I had prepared almost nothing to say. Everything I thought about saying was boring, so I decided the best way to approach the activity was to just get people started on it. Luckily for me, the group was ready to jump right in. I encouraged people to try the most symmetric shapes first, but other than that, I didn’t have to give them many suggestions.